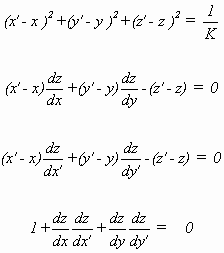
3.3 Die Bianchi- und die Lietransformation
Nachdem MINDING 1839 gezeigt hatte, daß sich zwei Flächen konstanter Gaußscher Krümmung auf unendlich viele Arten aufeinander abwickeln lassen, bewies BONNET 1867, daß jede Fläche konstanter Gaußscher Krümmung auf ¥ 1 viele Flächen gleicher Krümmung abgewickelt (oder verbogen) werden kann [Lie 1880a]. Damit war gezeigt, daß es mindestens ¥ 1 verschiedene pseudosphärische Flächen gleicher Krümmung gab und somit ¥ 1 Lösungen der SG-Gleichung. Die Integration der SG-Gleichung und damit die Bestimmung der Raumformen aller pseudosphärischen Flächen mittels der allgemeinen Lösung der SG-Gleichung gelang jedoch zunächst nicht [Lilienthal 1903]. Schließlich gelang eine Integration der SG-Gleichung vermöge der Bäcklundtransformation. Verfolgt man die Entstehungsgeschichte der Bäcklundtransformation, so fällt auf, daß sie durch das Zusammentreffen zweier zunächst unabhängiger "Strömungen" entstand: einer geometrischen und einer analytischen. In Frankreich und Italien entwickelte sich in den siebziger Jahren des vorigen Jahrhunderts die Idee der Flächentransformation anhand rein geometrischer Überlegungen. Zu erwähnen sind hier ALBERT RIBAUCOUR (1842 - 1893) und LUIGI BIANCHI (1856 - 1929). Auf der anderen Seite entwickelten in Norwegen und Schweden in der gleichen Zeit SOPHUS LIE (1842 - 1899) und ALBERT VICTOR BÄCKLUND (1845 - 1922) Erweiterungen von LIEs Theorie der Kontakttransformationen erster Ordnung und ihre Anwendungen auf Differentialgleichungen. Die Veröffentlichung von BIANCHIs Flächentransformation schließlich brachte die Synthese der beiden Strömungen, indem LIE und BÄCKLUND die Bianchische Transformation in ihre Gedanken einbeziehen konnten und BÄCKLUND aus ihr seine eigene Transformation entwickelte. Die grundlegende Idee, daß die Anwendung von Kontakttransformationen höherer Ordnung auf Differentialgleichungen möglich und erfolgversprechend sei, stammte von LIE, der sie 1874 als zwei Fragen formulierte [Lie 1874]. Direkt darauf wurde die Verallgemeinerung von BÄCKLUND realisiert, der Kontakttransformationen höherer Ordnung behandelte [Bäcklund 1874 und 1876]. Eine genaue Beschreibung dieser Abhandlungen findet sich in [And., Ibr. 1979].
Einige Jahre vor der Entstehung dieser Ideen der beiden Skandinavier gelang es RIBAUCOUR mittels rein geometrischer Überlegungen zu zeigen, daß es eine Konstruktion gibt, die eine pseudosphärische Fläche in eine andere überführt [Ribaucour 1870]. In der Übersetzung von [Lie, Bd. III S.733] lauten RIBAUCOURs Gedanken:
"Hat man eine Fläche von der konstanten Krümmung -1/a2 und beschreibt man um jeden ihrer Punkte in der zugehörigen Tangentialebene einen Kreis von konstantem Halbmesser, so werden diese Kreise von ¥ 1 Flächen orthogonal geschnitten, und zwar haben diese ¥ 1 Flächen wieder die konstante Krümmung -1/a2 und gehören einem dreifach orthogonalen System an. Auffallend ist es, daß Ribaucour sagt, der Halbmesser der Kreise sei gleich der Krümmung der Ausgangsfläche, während er doch gleich a gewählt werden muß."
Damit war deutlich geworden, daß ein Weg zur Bestimmung der allgemeinen Form von pseudosphärischen Flächen darin lag, bekannte Flächen durch Transformationsmethoden in andere zu überführen und damit von speziellen Lösungen der SG-Gleichung zur allgemeinen zu gelangen. LUIGI BIANCHI sagte 1910 hierzu [Bianchi 1910, S. 456]:
"Die wichtigsten Fortschritte in der Theorie der Flächen konstanter Krümmung sind mittels Transformationsmethoden erzielt worden, die es ermöglichen, aus einer bekannten Fläche konstanter Krümmung unendlich viele neue Flächen derselben Art abzuleiten, und zwar durch einfache algebraische Operationen und Differentiationen."
BIANCHI veröffentlichte 1879 in seiner "Tesi di abilitazione" eine Flächentransformation, die, wenn nicht gleich der RIBAUCOURschen, ihr doch sehr ähnlich ist. Sie überführt eine bekannte pseudosphärische Fläche in ¥ 1 viele neue [Bianchi 1879]. Er nannte sie Komplementärtransformation, weil in ihrer geometrischen Interpretation die Transformierte und die Ausgangsfläche die beiden Mäntel der Evolute einer dritten Fläche sind. BIANCHI beschrieb die geometrischen Gedanken seiner Transformation etwas anders als RIBAUCOUR [Bianchi 1880, S.577]:
"Man betrachte auf einer Fläche von constanter negativer Krümmung
-1/R2 ein System von parallelen geodätischen Linien und trage auf jeder Tangente dieser Linien vom Berührungspunkte aus die constante Strecke R ab. Der Ort der Endpunkte dieser Strecken ist mit derselben constanten Krümmung -1/R2 behaftet."
D.h., daß jedem Punkt der gegebenen Fläche je ein Punkt auf der transformierten Fläche zugeordnet ist, und daß die Tangentialebenen entsprechender Punkte senkrecht aufeinander stehen. Damit war eine Methode gefunden, aus einer bekannten pseudosphärischen Fläche auf festgelegtem Wege eine neue zu finden. Durch unendlichfache Anwendung der BIANCHIschen Transformation konnten ¥ 1 neue pseudosphärische Flächen gefunden werden.
BIANCHIs Transformation wurde sofort von LIE aufgegriffen. LIE war es, der sie zuerst erläuterte und in einer Reihe von Publikationen analysierte [Lie 1880 b-d]. Mit ihrer Erweiterung durch die Auto-Bäcklundtransformation der SG-Gleichung erlangte die BIANCHIsche Transformation ihre heutige Bekanntheit. Im Jahre 1881 erfuhr LIE von der Arbeit RIBAUCOURS, der LIE die Priorität an der heute sogenannten Bianchitransformation einräumte. Im Dezember 1881 schrieb LIE an FELIX KLEIN, mit dem er einen regen Briefkontakt, vor allem über seine mathematischen Überlegungen, unterhielt [Lie, Bd. III S. 733]:
"Ich habe eben einen interessanten Brief von Ribaucour, der eben eine große Arbeit über Minimalfl. produziert. ... Ribaucour schickt Dir einen freundlichen Gruß durch mich. Er ist Ingenieur und hat wenig Zeit zu der Mathematik, in der er nichtsdestoweniger sehr originelle Sachen produziert hat. Unter anderm hat er längst den Satz von Bianchi über Fl. konst. Kr., der mir so nützlich gewesen ist, in den Comptes Rendus publiziert, ohne indeß, wie ich glaube, auf seine Tragweite zu insistieren."
Hätte LIE vor 1880 von RIBAUCOURs Transformation erfahren, hätte er ihr evtl. mehr Geltung verschafft. So allerdings war es BIANCHIs Transformation, die er bekannt machte und zu deren Bedeutung er bemerkte [Lie 1880b, S.282]:
"... Hieraus folgt, daß die successive Ausführung von Bianchis Operation zur Bestimmung von Flächen konstanter Krümmung ... nur eine Reihe Quadraturen verlangt. Hierdurch erhält die schon von Bianchi gestellte Frage, ob man durch successive Ausführung seiner Operation aus der Pseudosphäre ... jede andere derartige Fläche herleiten kann, eine fundamentale Wichtigkeit für die Theorie dieser Flächen."
BIANCHI selber hatte 1879 keine analytische Form seiner Transformation angegeben. 1880 wurde jedoch von LIE eine Form angegeben [Lie 1880b], die BIANCHIs geometrischer Darstellung entsprach:
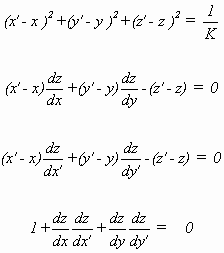
Die erste Gleichung sagt aus, wie ROELCKE in [Roelcke 1907] zusammenfaßte, daß zu jedem Punkt P = P(x,y,z) der gegebenen Fläche ein anderer Punkt P = P´(x´,y´,z´) auf der transformierten Fläche gehört, der von ihm die konstante Entfernung ô Kô -1/2 hat. Aus der zweiten und dritten Gleichung ersieht man, daß P´ auf der zu P gehörigen Tangentialebene der ursprünglichen Fläche und ebenso P auf der zu P´ gehörigen Tangentialebene der transformierten Fläche liegt. Die vierte ist die Bedingung dafür, daß die entsprechenden Tangentialflächen senkrecht aufeinander stehen.
Etwa zeitgleich mit BIANCHI fand LIE 1879 eine andere Transformation, die allgemeiner als BIANCHIs Komplementärtransformation ist. Lie hierzu [Lie 1879]:
"Bezeichnet man mit u und v die Bogenlängen der Haupttangentenkurven einer Fläche konstanter Krümmung, mit Φ den Winkel zwischen zwei einander schneidenden Haupttangentenkurven, so besteht nach einer Bemerkung von Bonnet eine Gleichung der Form:
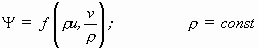
Ist nun Φ = f(u,v) eine bekannte Lösung dieser partiellen Differentialgleichung, so ist
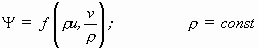
eine allgemeinere Lösung. Infolge derselben können aus einer vorgelegten Fläche immer ¥ 1 neue derartige Flächen hergeleitet werden."
LIE hatte sich, seit er die Arbeit von BIANCHI von 1879 erhalten hatte (spätestens im April 1880 [Lie, Bd. III, S.726]) intensiv mit BIANCHIs Transformation auseinandergesetzt. Und er kam zu folgendem Ergebnis, das er 1880 in einem Brief KLEIN mitteilt [Lie, Bd. III, S.732]:
"Ich betrachte es als sicher, daß die Vereinigung von Bianchis und meinen Untersuch. die allgemeine Bestimmung aller Fl. konst. Kr. leistet. Mein Beweis für die Richtigkeit dieser Behauptung ist sehr weit ausgeführt, so weit, daß ich jedenfalls kaum zweifele. Aber wie gesagt, fertig ist der Beweis nicht, und es wird auch nicht leicht sein, ihn fertigzubringen."
In einem späteren Brief des gleichen Jahres an KLEIN bestätigte LIE seine Vermutung. Ähnlich veröffentlichte er es auch 1880 [Lie 1880b]. Doch den Beweis veröffentlicht LIE erst 1883 [Lie 1883], kurz nachdem BÄCKLUND seine Transformationsmethode veröffentlicht hatte, die die Bestimmung aller pseudosphärischen Flächen erlaubt.
Weiter mit Kapitel 3.4: Die Bäcklundtransformation