4.3 Die Lösung der Sinus-Gordon-Gleichung
Nach diesen ersten vielversprechenden Lösungsansätzen der SG-Gleichung gerieten SEEGERs Arbeiten erst einmal ins Stocken. Rückblickend aus dem Jahre 1983 beschrieb er selber seine damalige Situation [Seeger 1983, S. 590]:
"Nach der damaligen Ansicht erschien es fast aussichtslos, nach echt zweidimensionalen Lösungen (d.h. nicht auf ein eindimensionales Problem zurückführbaren) strengen Lösungen einer nichtlinearen partiellen Differentialgleichung zweiter Ordnung wie Gleichung (4.11) zu suchen. Zu jener Zeit war das Denken der theoretischen Physik, wohl nicht zuletzt unter dem Eindruck der damals gerade erzielten Erfolge der Störungsrechnung mit Renormalisierung bei der Quantenelektrodynamik, ganz auf die Methoden der Linearisierung der Störungsrechnung abgestellt. Dementsprechend entwickelte ich in meiner Dissertation verschiedene Verfahren zur störungstheoretischen Behandlung von Gleichung (4.11) und von gewissen Erweiterungen." (Anmerkung: Zu diesen Erweiterungen zählt auch die Gleichung (4.10)). "Eine ganze Reihe der so gewonnenen Ergebnisse hat auch heute noch ihre Bedeutung; insbesondere bilden die Berechnungen des Schwingungsspektrums bei Anwesenheit von Versetzungen und die Behandlung von Streuung von Phononen an Versetzungen die Grundlage für die Thermodynamik der Solitonen."
SEEGERs störungstheoretische Behandlungen der SG-Gleichung finden sich in [See., Koch. 1951]. Die Störungsrechnung erwies sich für die SG-Gleichung als relativ leicht handhabbar. So bereitete z.B. die Lösung des Anfangswertproblems keine große Mühe. Da die Störungsrechnung bei stärkerer Nichtlinearität sonst in der Regel zu extrem komplexen Problemen führte, vermutete SEEGER, daß sich von dieser von ihm untersuchten Gleichung strenge Lösungen explizit angeben ließen, und er hielt Ausschau nach solchen. Diese Suche nach strengen Lösungen führte ihn 1950 zu den Arbeiten der Differentialgeometrie des letzten Jahrhunderts, die die SG-Gleichung ausführlich behandelten. Nach einem Vortrag des Autors im Jahre 1994 im MPI in Stuttgart erzählte Prof. SEEGER dem Auditorium in einer Anekdote, wie er zu diesen Arbeiten fand: Nach dem Krieg gab es an der TH in Stuttgart nur sehr wenige Professoren und infolge dessen auch nur wenige Vorlesungen. Daher war es üblich, alle angebotenen Vorlesungen zu hören, die mehr oder weniger in die Richtung des eigenen Studienfaches paßten. So hörte SEEGER eine Vorlesung über die Differentialgeometrie, die allerdings seiner Meinung nach schlecht war. Obwohl es kein Prüfungsfach war, interessierte ihn die Differentialgeometrie doch so, daß er sich ein Buch zuhilfe nahm, um dort mehr über die Differentialgeometrie zu lesen. Dieses Buch, es war die vierte Auflage von W. BLASCHKEs "Vorlesungen über Differentialgeometrie" [Blaschke 1945], war der Schlüssel, denn auf Seite 207 enthielt es eine Fußnote, die die SG-Gleichung erwähnte. Dort stand, daß auf Flächen von konstantem Gaußschen Krümmungsmaß K = -1 der Winkel zwischen den Asymptotenlinien der Gleichung (4.11) gehorcht, wenn man die Krümmungslinien der Flächen als Parameterlinien wählt. Das veranlaßte SEEGER, die ältere Lehrbuch- und Enzyklopädieliteratur zur Differentialgeometrie zu durchforsten, bis er durch die Übersetzung [Bianchi 1910] von BIANCHIs "Lezione di geometrica differenziale" auf die Bäcklundtransformation stieß.
SEEGER stellte fest, daß die von ihm bearbeitete Gleichung nicht nur die zu jener Zeit dank den Arbeiten von Bäcklund, Bianchi, Darboux und anderen Mathematikern wohl am gründlichsten untersuchte nichtlineare partielle Differentialgleichung zweiter Ordnung war, sondern darüber hinaus eine Fülle von physikalisch hochinteressanten Eigenschaften aufwies, die mit der Bäcklundtransformation zusammenhingen. Die Bedeutung dieser Entdeckung war SEEGER sofort klar [Seeger, pers. Mitt.]: Es gab Probleme in der Kristallphysik, die wesentlich von der Nichtlinearität gesteuert wurden. Schon BORN hatte darauf hingewiesen. Die Wärmeleitfähigkeit z.B., die mit der Störungstheorie behandelt wurde, oder die Infrarotabsorption. Das war auch mit ein Grund, warum die Störungstheorie so blühte. Aus bekannten Gründen hat die Störungstheorie jedoch nur einen beschränkten Wirkungsradius. SEEGER erkannte, daß mit der Bäcklundtransformation nun auch eine nichtlineare Gleichung exakt und allgemein gelöst werden konnte, und die Hoffnung bestand, daß die SG-Gleichung nicht die einzige integrable nichtlineare Gleichung ist. Das Zentrum der Anwendungsmöglichkeiten stellte für ihn das "nichtlineare Superpositionsprinzip" dar (Gleichung (3.15)). Damit war es möglich, nach je einmaliger Integration durch die Bäcklundtransformation, für zwei verschiedene Lösungen φ1 und φ2 , auf systematische Weise Familien von Lösungen mit unendlich vielen Mitgliedern zu generieren. Sie bildeten sich durch die Überlagerung gemäß dem Additionstheorem der Arcus-Tangens-Funktion aus, wobei selbst die Triviallösung φ = 0, ±π, ±2π,... als Ausgangslösung genommen werden konnte und physikalisch Interessantes ergab, nämlich die Überlagerung beliebig vieler Versetzungen beiderlei Vorzeichens mit beliebigen Geschwindigkeiten.
Das nun einsetzende schnelle Vorankommen SEEGERs und des mit ihm arbeitenden Diplomanden HANS DONTH in der Zeit direkt nach diesen Entdeckungen schilderte SEEGER selber [Seeger 1983, S. 591]:
"Mit den von der Differentialgeometrie bereitgestellten mathematischen Hilfsmitteln konnten mein Mitarbeiter H. Donth und ich in kürzester Zeit eine Fülle von Problemen lösen: Zusammenstöße zwischen Versetzungen gleichen oder entgegengesetzten Vorzeichens, Wechselwirkungen von Versetzungen mit Phononen und mit Wellenpaketen, allmähliches Entstehen von Versetzungspaaren über sog. "breather-Lösungen", Reflexion von Versetzungen an Kristalloberflächen u.a.m. Zu jener Zeit galt es, zumindest unter den sich mit Kristallphysik befassenden Physikern, als Dogma, daß Nichtlinearitäten mit Energieaustausch bzw. Energiedissipation verbunden sein müßten. Unsere Erkenntnisse widersprachen dem auf´s radikalste. Trotz der starken Nichtlinearität von Gleichung (4.11) hatten wir Lösungen gefunden, die selbst bei heftigster Wechselwirkung ihre wesentlichen Eigenschaften bewahrten, sich also wie Teilchen verhielten. Um die Verwandschaft der neuentdeckten Anregungsformen mit den wohlbekannten nichtwechselwirkenden Eigenschwingungen zu betonen, führten wir die Namen translatorische Eigenbewegungen für die versetzungsartigen Lösungen und oszillatorische Eigenbewegungen für jene wesentlich durch die Nichtlinearität von Gleichung (4.11) bedingten Lösungen ein, die wie Eigenschwingungen zeitlich periodisch waren. H. Donth und ich hatten ziemlich klare Vorstellungen einerseits von der weitreichenden Bedeutung unserer Resultate, andererseits aber auch von den Einschränkungen, denen sie unterlagen. Wir wußten, daß es eine Reihe von weiteren Gebieten der Festkörperphysik gab, die in mehr oder minder guter Näherung durch Gleichung (4.11) oder eine ihrer Erweiterungen beschrieben wurden, und bei denen mit dem Auftreten ähnlich verblüffender Phänomene zu rechnen war. Dazu gehörten der Ferromagnetismus, Phasenumwandlungen, sowie Kinken und Versetzungen."
Eine Weile nach diesen Entdeckungen erschien 1953 von SEEGER, DONTH und KOCHENDÖRFER der dritte Teil einer Veröffentlichungsreihe [See., Koch. 1950, 1951], [SDK 1953], der die Ergebnisse prägnant zusammenfaßte und aus heutiger Sicht einen vielzitierten "Klassiker" (citation classic, golden oldie) in der Literatur zu Solitonen darstellt. In diesen dritten Teil der Reihe flossen auch die Ergebnisse der Doktorarbeit SEEGERs [Seeger 1951] und der Diplomarbeit DONTHs [Donth 1951] ein. Der erste Teil beinhaltete im Wesentlichen die Ergebnisse aus SEEGERs Diplomarbeit [Seeger 1949]. Der zweite Teil befaßte sich mit der störungstheoretischen Behandlung der SG-Gleichung. Und der dritte Teil rundete die im ersten und zweiten Teil begonnene Behandlung der elliptischen Lösungen (4.14-18) der SG-Gleichung ab und gab eine erste Übersicht über die mit Bäcklundtransformation gewonnenen Lösungen. Die durch Bäcklundtransformation aus der Nullösung u0 = 0 gewonnenen elementaren Funktionen
![]() (4.19)
(4.19)
konnten SEEGER et al. mit Hilfe des Superpositionsprinzips einander überlagern und erhielten so aus zwei Lösungen der Form (4.19) eine weitere der Form
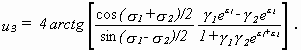 (4.20)
(4.20)
Durch die verschiedensten Kombinationsmöglichkeiten von σ1 , σ2 , γ1 und γ2 lieferten die so gewonnenen Lösungen (4.20) eine große Vielfalt an Interpretationsmöglichkeiten. Darunter führte der Fall γ1 = γ2 = 1 und σ1 konjugiert komplex zu σ2 in einem gewissen Bereich zu Wellenpaketen, die SEEGER et al. als Modell für die thermische Bewegung in Kristallen vorschlugen (s. Abb. 4.8).
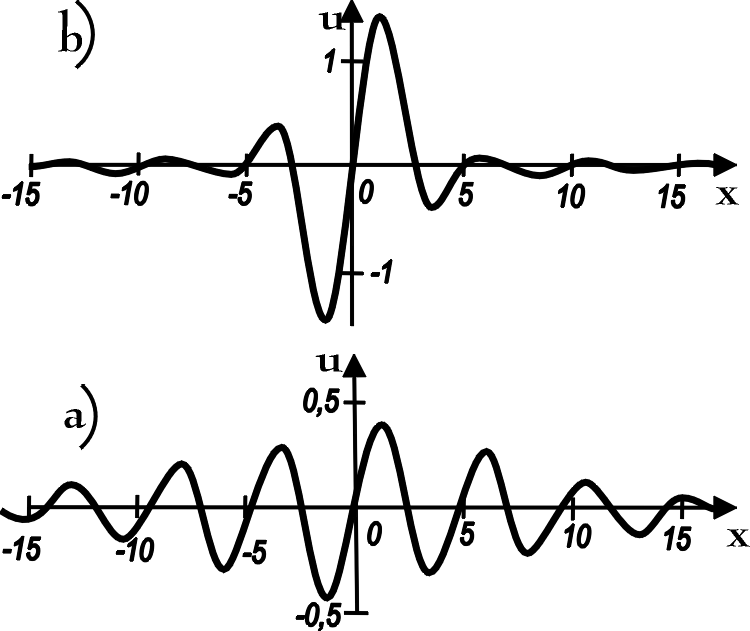
Abbildung 4.8:
Zwei Lösungen der Form (4.20) mit γ1 = γ2 = 1 und σ1 konjugiert komplex zu σ2 , aus [SDK 1953]. Sie bilden Wellengruppen, die SEEGER et al. als Modell für die thermische Bewegung in Kristallen vorschlugen.
Damit war es möglich, mit den Lösungen einer einzigen Gleichung, der SG-Gleichung, die Überlagerung von wandernden Versetzungen im thermisch angeregten Kristall zu modellieren. Wie SEEGER et al. auch in einer Abbildung zeigten (Abb. 4.9), fand zwar heftige Wechselwirkung zwischen Versetzung und Wellenpaket statt, der Teilchencharakter beider blieb jedoch vollständig erhalten, wie auch Energie, Wanderungsgeschwindigkeit und Form. Damit war dem herrschenden Dogma, daß bei Nichtlinearität Energiedissipation stattfinden muß, auf das heftigste widersprochen.
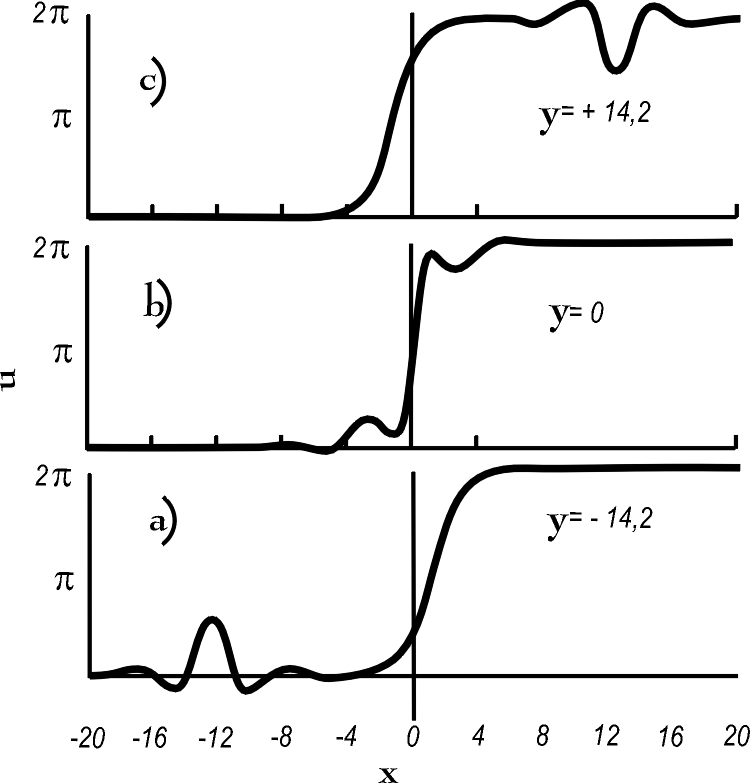
Abbildung 4.9:
Eine Wellengruppe durchdringt eine ruhende Versetzung. a) vor, b) während und c) nach der Durchdringung [SDK 1953]. Diese Abbildung zeigt die später so wichtig werdende Kollisionseigenschaft der Lösungen der SG-Gleichung.
Trotz der nichtlinearen Kraftgesetze war bei kontinuierlicher Behandlung des eindimensionalen Kristalls eine kontinuierliche Bewegung ohne Energiezufuhr möglich. Bei Berücksichtigung der diskontinuierlichen Struktur ergab sich hingegen eine Energiedissipation, wie SEEGER et al. am Ende ihres Artikels [SDK 1953] bemerkten, aufgrund der Wanderungsenergieschwelle, die die Versetzung überwinden muß. Dabei kommt es zu einer periodischen Änderung der Versetzungslänge und Versetzungsgeschwindigkeit, und damit zur Aussendung elastischer Wellen.
Die Arbeiten SEEGERs et al. schlugen keine hohen Wellen; die Reaktion darauf war eher verhalten [Seeger, pers. Mitt.], wie so oft bei Arbeiten, die dem Hauptstrom vorauseilen. Die Einmaligkeit der darin enthaltenen Entdeckungen wurden eben auch als "einmalig" betrachtet, d.h. als eine einzelne und daher unwichtige Kuriosität ohne allgemeine Bedeutung. Da die Solitonenlösungen spezielle Lösungen der partiellen Differentialgleichung sind, wurde vermutet, daß ihnen auch spezielle Anfangsbedingungen zugrunde liegen, die im Vergleich zum Anfangswertproblem eine eher untergeordnete Rolle spielen. Und die konkreten Anwendungen der SG-Gleichung, die sich im Jahre 1953 noch auf die Versetzungen im Kristall und deren thermische Bewegung beschränkten, waren nicht zahlreich genug, nicht allgemein genug, um große Durchschlagskraft zu erzielen. Diese wäre aber nötig gewesen, um die "Hemmschwelle" nichtlinearer Gleichungen in der Physik überwinden zu können. Die Bedeutung des "nichtlinearen Superpositionsprinzips" wurde nicht erkannt, da es eher als mathematisch interessant als für die Physik von Nutzen eingestuft wurde. Die mit dem Superpositionsprinzip zusammenhängenden Phänomene, die Teilchenartigkeit der Lösungen, hätten in Verbindung mit der Anwendbarkeit der SG-Gleichung und ihren Lösungen auffallen müssen, doch die Anwendungen schienen noch zu gering, man maß ihnen "singulären Charakter" zu. Daß das Superpositionsprinzip eine Art Erzeugungsoperator war, konnte noch nicht recht auffallen. Denn die zweite Quantisierung war in den fünfziger Jahren noch viel zu unbekannt, um das Superpositionsprinzip mitreißen zu können. Die Feldtheoretiker waren sich zu der Zeit noch nicht im Klaren, was das heißen konnte. Außerdem war der Bezug der SG-Gleichung zur Feldtheorie nicht zu erkennen; diese war ja erst in der Entstehung begriffen.
Um vom allgemeingültigen Charakter der entdeckten Eigenschaften der SG-Gleichung zu überzeugen, suchten SEEGER et alias in der folgenden Zeit nach weiteren Anwendungen und auch nach weiteren nichtlinearen Gleichungen mit analogen Eigenschaften. Das nichtlineare Superpositionsprinzip war solch eine Eigenschaft. Um die physikalische Relevanz zu wahren, sollten diese Gleichungen auch lorentzinvariant sein. Die Suche SEEGERs konzentrierte sich also auf Gleichungen der Form uxx - uyy = f(u), die das Superpositionsprinzip erfüllten. In den Folgejahren fand sich jedoch keine einzige weitere Gleichung dieser Art. Durch diesen Mangel an Anwendungen konnte SEEGER seine Entdeckungen, die besonderen Eigenschaften des Modells der Versetzungen und die Integrabilität der dazugehörigen nichtlinearen partiellen Differentialgleichung, nicht zur Ausbreitung bringen. In Stuttgart jedoch wurde in den folgenden Jahrzehnten an dem hoffnungsvollen Modell weiter gearbeitet. Weitere physikalische Anwendungen für das Modell der Versetzungen wurden gefunden [Seeger 1955], insbesondere die Beschreibbarkeit der Solitonen durch die Thermodynamik [Donth 1957], [See., Sch. 1966], und die Stuttgarter Schule um ALFRED SEEGER erlangte eine Führungsposition auf dem Gebiet der Versetzungen.
Weiter zu Kapitel 5: Der Übergang von der frühen zur klassischen Geschichte der Solitonentheorie