The History of the Early Period of Soliton Theory
Markus Heyerhoff,
[More detailed texts, in German]
The theory of soliton systems today touches an enormous range of theories and methods in various fields of mathematics and allows numerous applications in many areas of natural sciences from physics to biology and engineering. This multidisciplinary character of soliton theory can be traced back to its earliest days. Soliton theory has different and independant beginnings in fields as far apart as hydrodynamics, solid state physics, field theory, differential geometry and numerics. These different beginnings will be roughly scetched here. In all these areas the soliton theory at the beginning focussed more on the soliton than on soliton equations (or even systems of soliton equations). Even in differential geometry the interests of mathematicians were more directed towards the geometric interpretation of (what later became) the solitons: the pseudospherical surfaces. The equations governing these surfaces were of course studied with great care, but more as means to an end. The theory of soliton systems of today therefore started as theory of solitons. That began to change with the connection of the former independant roots of the "early period of soliton theory" and the rapid spreading of the new constituted soliton theory from 1967 on. There the early period ended and classical soliton theory began.

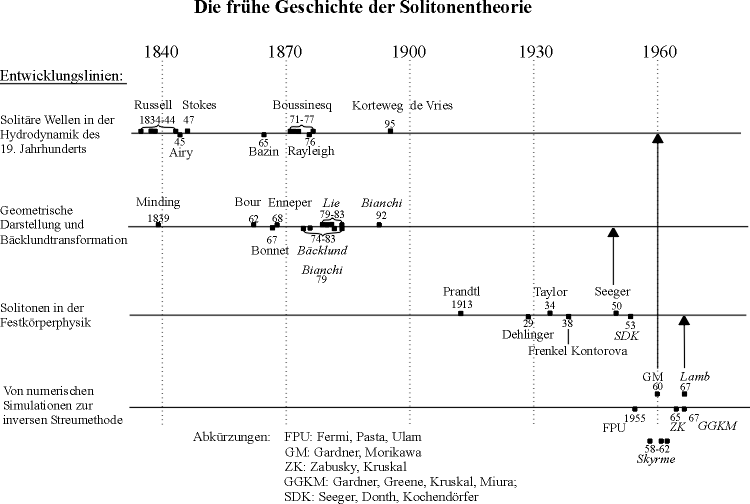
Figure 1:
Overview over the early period of soliton theory. Arrangement in four"lines of development" which merge into classical soliton theory from 1950 on. Within these lines the most important contributions to soliton theory are shown. The sequences of papers which success one another dealing with the same subject offer the arrangement in the four lines of development: one in hydrodynamics, one in differential geometry, one in solid state physics and one in numerics.
The soliton theory is a scientific discipline which lies in mathematics as well as in physics. And again not only in one area of mathematics or physics but in various different disciplines there. And the curious thing is that it shows in all these different areas different faces. In the history of soliton theory these different faces existed from the beginning on. And the effect was, that for over 130 years no one investigating the solitary wave or a soliton equation was thinking of connecting these different faces in the different areas of science to one theory.
A rough survey over the early history of soliton theory can be seen in figure 1. There the most important contributions to soliton theory can be found. The sequences of papers which success one another dealing with the same subject offer the arrangement in "lines of development". It is interesting to see how many runs of soliton theory failed to establish it´s effects in science until the break through took place in the seventies of this century. From then on the discipline "soliton theory" combined all the former independant roots and became what it is today. Now soliton theory connects several branches of science, it is interdisciplinary. The very beginnings of soliton theory started in mathematics, mathematical physics, theoretical physics and experimantal physics. During its early history the several at first independant aspects of soliton theory developed to a main frame. The most different "lines of development" united.
The early period of soliton theory began with the discoveries in experimental hydrodynamics in 1834 [2] and ended with the discovery of the inverse scattering transformation method (IST) in 1967 [3]. This is the historic region where apart from the main stream of developments single papers dealing with themes from what is now soliton theory showed up. But soliton theory did not yet exist. There was no idea, no conception of it, no system of terms. With the discovery of the inverse scattering theory (IST) by GARDNER, GREENE, KRUSKAL and MIURA in 1967 [3] one began to recognize the connections between the different branches. A search for new aspects began and the new discipline "soliton theory" started constituting. The formal acceptance soliton theory found in 1973 when it entered the subject index of Physics Abstracts. The section of time beginning with 1967 can be called the "classical period" of soliton theory. The theory and its conception become worked out in detail. This period of time seems not yet completed. It is not at all possible to survey the section of the classical period because a soliton-boom followed the paper by GARDNER et al. at the end of the sixties. Until now many thousands of papers exist around the soliton theory.
Solitons are governed by nonlinear equations. In physics soliton theory was in opposition to linearity since its earliest days. Although nonlinearity was present in almost every branch of physics one considered the few known solutions of some nonlinear differential equation until the 60´s of this century in physics far less important as solutions of linear equations. Firstly because within small boundaries almost everything can be linearized more or less. And secondly linearity means additivity without disturbing interaction. Therefore the oppinion was prevailing that nonlinear equations would not be able to serve in particle models because the solutions of nonlinear equations have to interact violently when hitting each other. And this violent agitation was thought to destroy the initial properties of the solutions. That changed with the dicoveries of soliton theory.
The name "soliton" appeared the first time in 1965 [1]. It was given to solutions of the KdV by MARTIN KRUSKAL and NORMAN ZABUSKY. They gave the name because of the particle properties of these solutions on the one hand and the solitary wave on the other hand. The expression "solitary wave" dates back to 1837 and was given by JOHN SCOTT RUSSELL, an engineer and artist in ship building, to a solitary water wave [2]. Kruskal and Zabusky however had chosen "solitron" instead of "soliton" for the name of the wave, for putting it into the same zoo of particle names as electron and neutron and so on. But the name "solitron" was a trade mark and therefore not suitable.
When a scientist familiar with soliton theory is asked about its history the first names he remembers is usually RUSSELL and KORTEWEG / DE VRIES. Many details of this most famous and oldest root of soliton theory, where shallow water waves became investigated, are reviewed by ROBIN BULLOUGH [4, 5]. In a canal a solitary wave can travel over long distances. It "presents itself as a solitary progressive elevation of the surface of a quiescent fluid, neither preceded nor followed by any secondary or successive phenomena," as RUSSELL describes the wave in 1837 [2] or 1838 as "a heap of a well-defined form" [6]. As we know today the shape corresponds to a solution of the KdV, where ξ is a constant:
![]()
The famous french mathematician JOSEPH LOUIS LAGRANGE wrote in his book "Méchanique analytique" in 1788 that some waves in canals have to be described with nonlinear equations of motion. But for simplification he only concentrated on linear equations and got for result the well known linear velocity of the waves
![]()
where g is the gravitation constant and h the depth of the water.
The first one investigating these types of waves more carefully was the scottish engineer and ship designer JOHN SCOTT RUSSELL. In 1834 he became the order to investigate the Union Canal, which is a small canal between Edinburgh and Glasgow for the purpose of using it with fast steam boats. In summer 1834 he noticed a single wave coming from a fast travelling boat which had suddenly stopped [2, 6, 7]. RUSSELL was immediately fascinated by this wave, because he realized its unusual qualities distinguishing "the wave" as he called it at first from other waves. The wave travelled solitarily and without change of form over a long distance. RUSSELL was filled with enthusiasm by his discovery so that he made many experiments on this wave for example the following one: With horses he pulled a few larger boats dozens of times very fast into one direction. Each one sending a solitary wave to one of the closed ends of the canal transporting a portion of water to this end. In the evening Russell observed, that the level of water at this end got rised eighteen inches and at the other end it had sunk the same amount [8, 9]. This way RUSSELL showed the transporting quality of the wave and called it "the great wave of translation". RUSSELL was not a mathematician or physicist. His mathematical tools were rather poor. But he had the experiment as tool for his research and used it extremely well. In over a hundred experiments he investigated the properties of his wave: the lack of dispersion, the uniformness, the collision properties and the velocity v of the wave
![]()
The velocity deviated from the known linear velocity and RUSSELL understood what that meant. The wave must be of a completely different manner than usual waves because the velocity depended on the amplitude H of the wave. But immediately after RUSSELL had published his results he was attacked by physicists, firstly by the famous GEORGE BIDDELL AIRY [10]. He misunderstood the whole phenomenon and did not trust RUSSELLs experiments. GEORGE GABRIEL STOKES was more careful and tried to come to RUSSELLs results analytically [11]. But he was only able to get more or less linear results and formulated some doubts about RUSSELLs. Here one can see the problems of nonlinearity. Nonlinear partial differential equations are difficult to solve, and this is probably one reason why they were almost ignored in physics for a long time. Now a long discussion started between physicists and mathematicians. And soon RUSSELL, tired of discussions, retired from science and started to build large steam ships with great success.
In 1872 the french mathematician JOSEPH DE BOUSSINESQ wrote an analytical treatment on waves in canals and gave an equation for the solitary wave which was later named after him [12]. He indicated a solution of his equation which had the shape of the solitary wave and which corresponded to RUSSELLs velocity of the wave. Funny enough the article was almost ignored in England. But in 1876 LORD RAYLEIGH published an article on the same subject [13]. In rather long-winded calculations he came to solutions quite similar to BOUSSINESQs which showed the properties of RUSSELLs wave. That could have cleared the whole discussion. But instead a long quarrel started about the stability of RAYLEIGHs solutions and their velocity, which differed a little from RUSSELLs and others due to a little difference in RAYLEIGHs ansatz. The quarrel was finally terminated by the Amsterdam professor for mathematics DIETERIK KORTEWEG and his PhD student GUSTAV DE VRIES in 1895. They discussed the whole problem and formulated the equation which is now named after them Korteweg-de Vries equation [14]. And they indicated solutions which showed exactly the qualities Russell had described 50 years earlier. Now RUSSELLs experiments had found their theory and one could think that scientists would continue to investigate the extraordinary results of this theory. But that did not happen. The phenomenon of the solitary wave vanished from the table of science for many decades.
Another important root of soliton theory lies in differential geometry. About 20 years ago it was discovered that all soliton equations show an interesting quality: Their solutions describe surfaces with special curvature properties. In differential geometry of the last century these surfaces were studied, among them pseudospherical surfaces i.e surfaces of constant negative Gaussian curvature.
In his paper of 1839 FERDINAND MINDING investigated such surfaces [15]. After his proof that surfaces of the same constant Gaussian curvature can be put into a one-to-one correspondence he used among others rotational surfaces of constant negative Gaussian curvature as examples for his result and gave a detailed description of them.
23 years later it was EDMOND BOUR [16] who gave a "new and surprising" equation for such rotational surfaces: the today so called sine-Gordon equation (sG)
![]()
where Φ is the angle between the asymptotic lines of the surface. BOUR mentioned the sinus-amplitudinis solutions of the sG but gave no further description of the equation. A little later OSSIAN BONNET in 1867 [17] and ALFRED ENNEPER in 1868 [18] mentioned the sG as an equation for pseudospherical surfaces. Of course they could not know, that this equation was something special or even solitonic.
In the seventies of last century the question arose to find all pseudospherical surfaces and the answer found was this: via surface transformations. That means transformations which transform one known pseudospherical surface into another. The first one successfull in finding such a transformation was the italian mathematician LUIGI BIANCHI in 1879. With his transformation he was able to find from one known surface one times infinitely new pseudospherical surfaces [19].
One year after BIANCHI the norwegian mathematician SOPHUS LIE found another transformation with the same properties [20]. This transformation is known under Lie transformation and physicists call it Lorentz transformation. LIE reformulated BIANCHIs transformation too and had the good guess, that these two transformations together could form a third transformation with which one was able to find all pseudospherical surfaces [21]. In 1883 the swedish mathematician ALBERT VICTOR BÄCKLUND confirmed this by generalizing Bianchis transformation into the today so called Bäcklund transformation [22]. In 1889 GASTON DARBOUX [23] put it into a form which is used today:
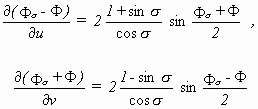
From a known solution Φ of the sG, it can even be the trivial solution Φ = 0, infinitely many solutions Φσ can be obtained by using this transformation due to the free parameter σ. The condition of integration is the known sG. Again the Bäcklund transformation can be used more than once taking the former result Φσ as the new Φ and obtaining another Φσ. This can be done infinite times obtaining twice infinite solutions. In this way the sG is not only the eldest known soliton equation but already in the last century proved to be integrable.
BIANCHI found in 1892 [24] that by multiple application of the Bäcklund transformation the result is the same no matter which succession for the transformations is chosen:
![]()
In the proof of this BIANCHI formulated the following equation:
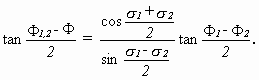
It says that if two Bäcklund-transforms Φ1 and Φ2 of a starting solution Φ are known, one can obtain a third solution Φ12 only by algebraic operations. That showed that no integration of the Bäcklund transformation is needed anymore exept for the first ones. For physicists this equation is interesting because the equation shows that for the solutions of the sG a "nonlinear superposition principle" exists in the way the equation shows.
The sG and its Bäcklund transformation are the only discoveries of differential geometry which played a major role in the early period of soliton theory. Later, in the classical period of soliton theory, many more soliton equations and -techniques were discovered. And some also showed to have roots in differential geometry of the last and the beginning of this century. A few of these I shall touch here:
* In his well known treatise on surfaces of constant mean curvature JULIUS WEINGARTEN mentioned the hyperbolic sinh-Gordon equation in 1863 [25]
![]()
in the form
![]()
which was shown to have soliton solutions in 1985 [26].
* As S. P. TSAREV found out in 1992 [27] the well known Bullough-Dodd equation
![]()
was already treated by the romanian mathematician G. TZITZÉICA in 1910 [28] in the form
![]()
TZITZÉICA also gave the respective linear problem as well as the proper Bäcklund transformation for it.
* From B. A. DUBROVIN [29] comes the hint that the "three wave system", a soliton system integrable by the IST, coincides with the Egorov coordinate systems. TSAREV [27] mentioned that this kind of systems was initiated by DARBOUX in 1866 (who proposed in 1910 to call it Egorov type systems [30]) and continued by D. TH. EGOROV in 1901 in his thesis [31]. LUIGI BIANCHI found the Bäcklund transformation for this problem in 1915 [32] and established the superposition formula for it.
* In 1882 Gaston Darboux [33] gave the basic proof for the today so called Darboux transformation. A detailed description of its history can be found in [34].
In a way the mathematicians of the last century entered much deeper into soliton theory than Russell 30 years earlier who had recognized the unusual features of the solitary wave. I cannot imagine a greater contrast in procedure within one discipline of science. In experimental hydrodynamics the attributes of solitons were discovered and described very exactly. But an equation did not exist at first because of the lack of mathematical capacity. In differential geometry some mathematics of the later soliton theory was derived in a precise manner, but no physical meaning could be recognized.
In this century the soliton theory took a new run to establish itself in physics. Many historical details of this line of development are reviewed by ALFRED SEEGER [35, 36].
This again complete different ansatz lies in solid state physics and dates back to 1913. In this time physicists thought about the atomic structure of matter, especially of metals. And a central question was, how the plastic deformation of metals took place in the crystal lattice of the metal, how the mechanism worked. The first ansatz in this field came from the german physicist THEODORE VON KÁRMÁN, who introduced a model given by LUDWIG PRANDTL in 1913 [37]. This and similar models of the atomic structure in crystals during the act of deformation were discussed widely. The one by G. I. TAYLOR [38], a british physicist, which followed an ansatz of ULRICH DEHLINGER from 1929 [39], again points towards the sG.
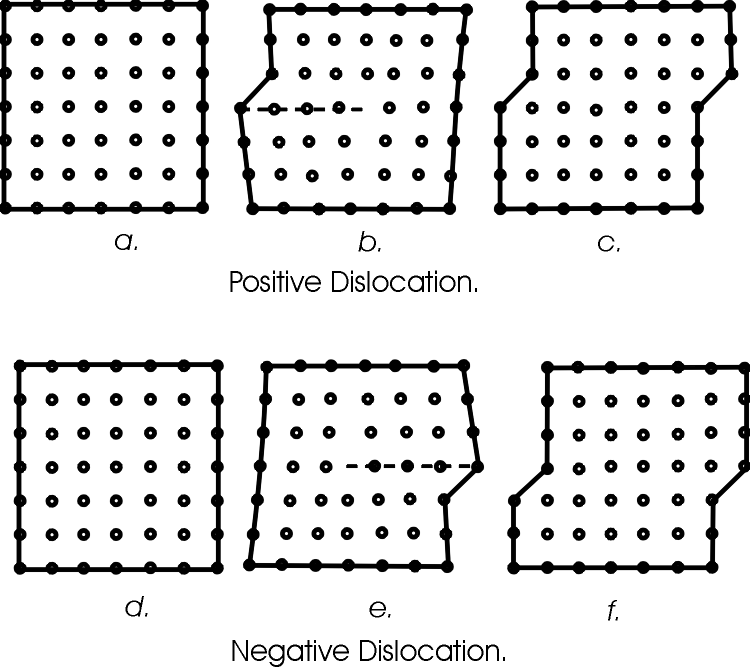
Figure 2:
Model for the mechanism of deformation of a crystal lattice by G. I. Taylor [38]
Figure 2 shows a crystal lattice. If one atom is pulled away, let´s say to the left, the others follow, each jumping into the new hole, the free lattice space of the neighbour atom. In this way a "dislocation" runs through the crystal. This model was widely discussed and improved by the Leningrad professor for theoretical physics JACOV ILICH FRENKEL and his assistant TATJANA ABRAMOVNA KONTOROVA in 1938 [40]. They continuized the Taylor model into the Frenkel-Kontorova model, where not only each atom moved alone over one lattice distance but many atoms formed a long dislocation line. In this way the dislocation becomes a wave of translation.
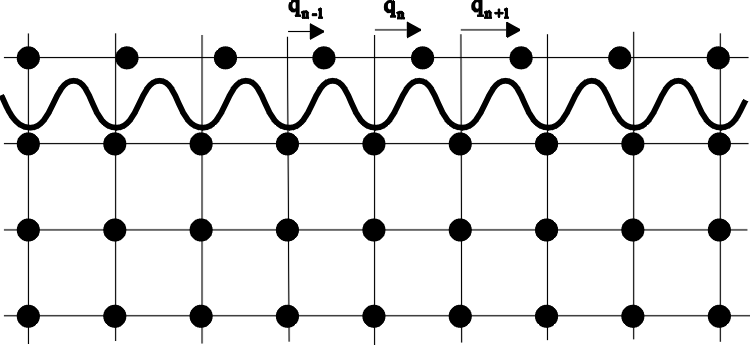
Figure 3:
The dislocation line of the Frenkel-Kontorova model [40].
FRENKEL suspected the solitonic character of his dislocation line because he assumed that the process of travelling through the crystal would happen without any losses of energy. This is equivalent to RUSSELLs solitary wave of translation which travelled over long distances without change of form and velocity. FRENKEL rewrote DEHLINGERs equation of motion from 1929 of a dislocation and included its dynamics which DEHLINGER had left out
![]()
qn : distance of the n-th atom from its equilibrium position
a : lattice constant
A, C : constants
The right side represents the force on the n-th atom. F results from the two neighbour atoms pulling from each side at the atom with a linear force (right term) and the line of atoms "underneath" the dislocation, assumed to be rigid, pulls at the n-th atom with a sinoidal potential. A careful look at this equation will uncover that a continuization of the space variable n leads directly to the sG. But FRENKEL and KONTOROVA did not carry out this real continuization. They implicitely assumed it in their way of solving the equation. So they arrived at the one-soliton solution of the sG.
The german physicists ULRICH DEHLINGER and ALBERT KOCHENDÖRFER assumed these travelling dislocactions to be of so great importance that they gave them the name "Eigenbewegungen" pointing out their similarity to the "Eigenschwingungen" which result from the quadratic potential of the quantum mechanical model of the atoms [41]. They assigned the task to generalize the Frenkel-Kontorova model to the physics student ALFRED SEEGER for diploma thesis in 1948. And he was the first, after having undertaken the continuization of the model, writing down the sG in a physical context. But although trying hard he was not able to integrate the equation.
Two years later, while he was working on his PhD thesis, by chance he came along the works of BIANCHI in differential geometry [42]. Now he had found the possibility to obtain the solutions of the sG by Bäcklund transformation and he investigated them carefully. While he was doing so he discovered their amazing qualities: the uniformness, their lack of dispersion and their collision properties. And amazing was Bianchi´s superposition principle because it showed that nonlinear equations could govern particles. In physics there still existed the dogma, that particle character only existed with linear waves due to lack of superposition for nonlinear waves. This was disproved now. SEEGER was able to solve the sG and he had recognized the unusual features of the solitary wave as well as RUSSELL 100 years earlier.
Actually, the soliton theory could have come to the decisive break through with the publication of these results by SEEGER et al. in 1953 [43] which occured only later in 1967 in the USA. From our position nowadays the discoveries around the KdV and the sG appear like a race of these two equations: Which one could establish soliton theory in the scientific world? And in 1953 the sG seemed to be miles ahead of the KdV which was completely forgotten by that time and not yet integrated. The discoveries in Germany around the sG in solid state physics could have been the ignition for soliton theory. But that did not happen. The scientific community was not interested in another nonlinear partial differential equation. Although SEEGERs discoveries were very promising there was not much attention payed to them because one could not find any generality in that case [44]. The effects found seemed to be singular in an ocean of problems and equations, they seemed to be without general significance. For the purpose to show the generality SEEGER searched for other equations which on the one hand fulfilled Bianchis superposition principle and on the other hand were Lorentz invariant as required for physical equations of that type. But he did not find any further equations and after a while he stopped working on this phenomenon and it became forgotten.
Even the complete independant discoveries in field theory by the british physicist TONY HILTON ROYLE SKYRME in 1962 could not prevent this. He proposed the sG for equation of motion of particles and interpreted the solutions being some elementary particles [45]. But he did not get through. So the sG fell into oblivion again.
But not for long. In 1955 the physicists ENRICO FERMI, JOHN PASTA and STANISLAV ULAM in Los Alamos had an enormous computer to their disposal. It was the MANIAC I the strongest computer existing at that times. Interested in the abilities of such machines they investigated systems without closed analytic solutions. And in their first numeric experiment they simulated 64 particles on a string coupled by quadratic forces [46]. If now one particle was hit out of its equilibrium position the physicists expected the energy to distribute into all the higher oscillation modes. This would be the normal process for nonlinear coupling. But instead the energy focussed on the ground mode again and did not disappear in distributing itself. FERMI, PASTA and ULAM could not really understand that process and did no further systematic investigations on it. But it activated additional studies. NORMAN ZABUSKY and MARTIN KRUSKAL, two american mathematicians, picked up the Los Alamos studies and in 1965 continuized the particles on the string to a continuum. And they showed that the continuum problem had the KdV for equation of motion. Their numerical experiments showed, that two solutions of the KdV penetrated through themselves undisturbed, like particles. Now the integration of the KdV became an interesting question. And as a consequence in 1967 a method for integrating the KdV was found: the IST.
In the race between the KdV and the sG the KdV started overtaking now. Its connection to the Schrödinger equation had pushed it forward a great deal. From now on the developments in soliton theory went blow on blow. More and more the connections between all these equations and theories became understood: integrability and the solitons. A new scientific discipline, the soliton theory, started to exist.