[Inhaltsverzeichnis]
2.2 Diskussionen über die Natur der solitären Welle
Als RUSSELL sich mit der Erforschung von Wellen
beschäftigte, war er damit in Europa keineswegs allein, sondern einer unter
vielen. Vielerorts in Großbritannien, Frankreich, Italien und im
deutschsprachigen Raum wuchs unabhängig voneinander das Interesse an der
Bewegung des Wassers. Und als Folge davon wuchs in dieser Zeit die Zahl der
Publikationen zu dem Thema. Die Zahl der wissenschaftlichen Arbeiten, die sich
mit Wellen auseinandersetzten, hatte zum Ende der dreißiger Jahre des 19.
Jahrhunderts zu wachsen begonnen und erreichte in den Vierzigern einen ersten
Höhepunkt [Catalogue 1909]. Untersucht wurden Wellen in verschiedensten Formen:
Schiffswellen, Meereswellen, Brandung, Flachwasserwellen, Kapillarwellen u.v.m.,
aber auch einzelne Wellen wie Gezeiten, Flutwellen in Flüssen, stehende Wellen
in Flüssen, Wellen, die sich durch Rückstau eines fließenden Gewässers
bilden und eben auch die von RUSSELL erstmals ausführlich beschriebene von ihm
so genannte solitäre Welle, die nicht wenig Aufmerksamkeit erhielt.
RUSSELLs Arbeiten trugen somit zum Wachstum des Interesses an Wellen bei. Dies
auch nicht zuletzt durch die mitreißende und klare Art seiner Darstellungen
1836, mit der er die British Association for the Advancement of Science für
"sein" Thema begeistern konnte. Später rief die zum Teil harsche
Kritik an RUSSELLs Arbeiten zur solitären Welle manche Kommentatoren auf den
Plan, die mit Stellungnahmen, mathematischen Herleitungsversuchen oder sogar
eigenen Experimenten versuchten, das neue Phänomen zu erklären. Daher gab es
in den folgenden Jahrzehnten recht viele Autoren, die sich mit der solitären
Wasserwelle auseinandersetzten.
Schaut man RUSSELLs vielfältige Arbeiten zu diesem Thema an,
so erheben sich kaum Zweifel an seinen Ergebnissen. Die Haupteigenschaften der
solitären Welle sind, wie in seiner Arbeit von 1844 deutlich wird, vielfach
überprüft und klar dargestellt. Diese Eigenschaften bedurften nun einer
theoretischen Erklärung. Und daß diese zu liefern kein leichtes Unterfangen
war, zeigen manche späteren vergeblichen Versuche, die keinen weiterführenden
Beitrag zur Erklärung der Welle zu geben vermochten. Solche Schwierigkeiten bei
der Erklärung führten auch zu Fehlschlüssen und diese wiederum zu Zweifeln an
der Richtigkeit von RUSSELLs Ergebnissen. Und nicht selten wurden RUSSELLs
Arbeiten verurteilt, weil die Eigenschaften der solitären Welle nicht
erklärbar schienen. Erschwerend kam hinzu, daß von anderen Wissenschaftlern
durchgeführte ähnliche Experimente nicht die gleichen Ergebnisse lieferten wie
RUSSELLs Experimente und damit zusätzlich Zweifel an RUSSELLs Ergebnissen
aufkommen konnte. Da der Mechanismus der solitären Welle nicht ganz verstanden
war, wurden bei Vergleichen zwischen manchen Experimenten wichtige Parameter
außer Acht gelassen, wie z.B die Wellenhöhe im Verhältnis zur Wassertiefe.
Die Gebrüder WEBER (s.o.) konnten durch eine zu große Wassertiefe in ihrem
Becken in einem ansonsten dem Russellschen sehr ähnlichen Versuchsaufbau keine
solitäre Welle beobachten. Versuche mit sehr geringer Wassertiefe lieferten
dagegen schöne negative solitäre Wellen, wie die des Amerikaners DYAR [Dyar
1843]. Schon 1843 und unabhängig von RUSSELL, wie es scheint, erforschte DYAR
die solitäre Welle in einem dem Russellschen sehr ähnlichen Versuchsaufbau: In
einer Wanne (3,33m Länge x 16cm Breite) wurde eine positive oder negative
solitäre Welle durch schnelles Eintauchen oder Herausziehen eines Gewichtes
erzeugt. DYAR nannte die solitäre Welle onde élevée bzw. onde
déprimée. Während es RUSSELL nicht gelungen war, eine negative solitäre
Welle ohne oszillatorische Wellen zu erzeugen (s. Abb. 2.7), beschrieb DYAR
seine negative Welle als exaktes Gegenbild der positiven. Da die ungleichen
Eigenschaften der negativen und positiven solitären Welle RUSSELL als ein
wichtiges Kriterium zur Unterscheidung der solitären von anderen Wellen diente,
konnte auf diese Weise eine wichtige Eigenschaft der solitären Welle in Frage
gestellt werden. DYARs Ergebnisse bei Kollisionsexperimenten stehen sogar im
direkten Widerspruch zu RUSSELLs. DYAR beschrieb alle Möglichkeiten der
Kollision, des Überholens, mit positiven, negativen oder beiden Arten von
Wellen. Immer ist sein Resultat, daß die Wellen nach gegenseitiger
Durchdringung unverändert fortlaufen. Bei RUSSELL war die negative Welle von
der sie überholenden positiven vernichtet worden. DYAR beschrieb die negative
Welle oder onde déprimée als gleichwertig der positiven. Weder DYAR
noch RUSSELL erkannten, daß für die Stabilität der negativen
"solitären" Welle deren Amplitude im Verhältnis zur Wassertiefe
maßgeblich ist, worauf KORTEWEG und DE VRIES 1895 aufmerksam machten [KdV
1895]. Je kleiner die Wassertiefe ist, desto weniger oszillatorische Wellen
zieht sie hinter sich her.
Der schärfste Angriff gegen RUSSELL erfolgte von GEORGE
BIDDELL AIRY (1801-1892). Der durch seine vielen erfolgreichen
wissenschaftlichen Aktivitäten sehr geschätzte Königliche Astronom und
Direktor des Observatoriums von Greenwich hatte eine lange theoretische
Abhandlung zu Gezeiten und Wellen verfaßt [Airy 1845]. In ihr ging er
kritisch auf die theoretischen Arbeiten von NEWTON, BERNOULLI, LAPLACE, LAGRANGE
und CAUCHY sowie auf die experimentellen Arbeiten der Gebrüder WEBER und
RUSSELL ein [Rouse, Ince 1957]. Was RUSSELL betrifft, bezog sich AIRY nur auf
dessen Arbeiten bis einschließlich 1840. Da RUSSELL in seiner Arbeit von 1844
auf AIRYs Abhandlung einging (wenn auch nicht namentlich, so doch deutlich
genug), ist davon auszugehen, daß AIRYs Abhandlung bis 1844 schon vorgelegen
hatte und AIRY keine Gelegenheit hatte, RUSSELLs spätere Ergebnisse zu
berücksichtigen. AIRYs Urteil über RUSSELLs Arbeit von 1837 ist nicht eben
schmeichelhaft [Airy 1845, S. 345, 350]:
"... it will be necessary, however, to make some
remarks upon Mr. Russell´s references to theory, because we believe that
anyone who should derive his first knowledge of the nature of waves from that
paper would receive from it a most erroneous notion of the extent of the
Theory of Waves at the date of those experiments. ... Meanwhile we shall
repeat our opinion of the great value of the experiments which we have
abstracted, but we must warn the reader against attaching any importance to
the theoretical expressions which are mingled with them in the original
account."
AIRYs Einwände gegen RUSSELLs theoretische Ausführungen
sind durchaus begründet. Denn von den wenigen kurzen Rechnungen, die RUSSELL
seinen Schlüssen hin und wieder anfügte, sind einige fehlerhaft; die meisten
sind verworren und kaum wirklich hilfreich. Doch nur selten drückte RUSSELL
seine Ergebnisse mathematisch aus. Seine Stärke lag in der Beobachtung und
Beschreibung des Beobachteten. Diese Beobachtungen lieferten ihm eine über
Jahrzehnte nicht wieder erreichte Kenntnis über "the nature of waves",
zumindest was die solitäre Welle betrifft. An einer anderen Stelle führte AIRY
aus [Airy 1845, S. 346]:
"We are not disposed to recognize this wave as
deserving the epithets "great" or "primary", ... and we
conceive that, ever since it was known that the theory of shallow waves of
great length was contained in the equation
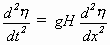
... the theory of the solitary wave has been perfectly well
known. ... There is one particular velocity (that defined by the equation c2
= gH) at which a free wave will travel along a canal of given depth
H."
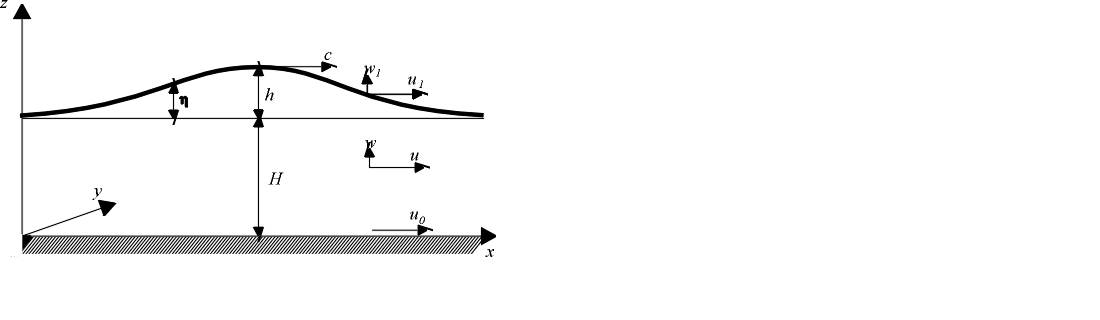
Abbildung 2.6:
Einheitliche Bezeichnungsweise, mit der in diesem Kapitel
alle Rechnungen und Ergebnisse der hier behandelten Abhandlungen dargestellt
werden:
x, y, z: rechtwinklige Koordinaten. Die (x,y)-Ebene fällt
mit dem Kanalboden zusammen
H: Wassertiefe des ungestörten Wassers
h: maximale Höhe der Welle
η(x): Oberfläche der
betrachteten Welle
c: Fortpflanzungsgeschwindigkeit der Welle
u(x,z), w(x,z): Bewegungsgeschwindigkeiten eines
Wassermoleküls am Ort (x,z)
u1(x,z), w1(x,z): ... an der
Wasseroberfläche
u0(x,z): ... auf dem Grund
AIRY war nicht bereit, in Erwägung zu ziehen, daß die
solitäre Welle ein in der Theorie noch unbekanntes Phänomen sein konnte, denn
er negierte die von RUSSELL gefundene Geschwindigkeitsformel c2 =
g(H+h), so wie er auch die von RUSSELL gefundene Andersartigkeit der
negativen solitären Welle nicht akzeptierte. Seine eigenen theoretischen
Erklärungen ließen keinen Raum für eine solitäre und gleichzeitig
formstabile Welle. AIRYs Gleichungen konnten nur harmonische Lösungen liefern,
die zum einen negative wie positive Wellen gleichwertig behandelten und zum
anderen entweder eine solitäre Welle zuließen oder zeitlich unveränderte
Wellen, aber niemals beides gleichzeitig. Unter der Annahme kleiner, oszillatorischer Wellen gelangte AIRY zu der
Wellengeschwindigkeit
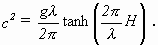 (2.3)
(2.3)
(AIRYs Begründungen von Annahmen, die zur
Aufstellung der Gleichungen nötig sind, und seine Herleitungen sind recht
langatmig und umständlich. Ihre Darstellung wird daher hier nicht wiederholt.)
Die Grenzfälle der Gleichung 2.3 gehen für sehr kleine bzw. sehr große
Wellenlänge λ in die seit GERSTNER
[Gerstner 1804] bzw. LAGRANGE [Lagrange 1788] bekannten Geschwindigkeiten über:
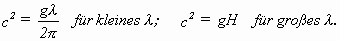
AIRY versuchte ferner die Bedingungen zu untersuchen, unter
denen eine solitäre Welle doch unverändert durch einen Kanal laufen könnte.
RUSSELL hatte immer periodische Funktionen für die Form der solitären Welle
angegeben, zuerst die Zykloide, dann den "verschobenen Sinus". Das
bedingt, daß die Funktion vor und hinter der Welle abgeschnitten wird, damit
sie außerhalb der Welle konstant ist. Das war sicherlich kein mathematisch gut
durchdachter Ansatz. Doch AIRY, der RUSSELLs mathematische Fähigkeiten so
schmähte, tappte nun mit seiner Erklärung der solitären Welle in die gleiche
Falle. Er unterstellte, daß eine unverändert laufende und solitäre Welle eine
scharfe Begrenzung haben muß, außerhalb derer die Wasseroberfläche auf
konstantem Niveau ruht, also die einzelne Welle durch eine diskontinuierliche
Funktion beschrieben wird. Ebenso wie RUSSELL hielt es AIRY generell für
sinnvoll, auch eine diskontinuierliche Funktion als Linearkombination von
Sinusfunktionen zu betrachten. Die Voraussetzung stetiger Anschlußbedingungen
an den Rändern der Welle führte AIRY dazu, notwendigerweise eine äußere
Kraft einzuführen, die auf die Welle wirkte. Ein gezogener Kahn z.B. könne
diese äußere Kraft ausüben und eine einzelne Welle aufrechterhalten, wie AIRY
annahm. Ohne eine äußere Kraft, so AIRY, konnte eine freie, einzelne und
unveränderte Welle nicht existieren. Im Hinblick auf RUSSELLs Experimente
konnte für ihn als einziger Ausweg die Annahme einer im Verhältnis zur
Wassertiefe sehr langen Wellenlänge gelten. Das jedoch führte ihn wieder
zurück auf die bekannte Geschwindigkeit der Welle c2 = gH. In
diesem Falle konnte sich AIRY die einzelne Welle als Linearkombination sehr
langwelliger Sinusfunktionen fast gleicher Wellenlänge vorstellen, was eine
sehr kleine Dispersion bedeutet hätte. Das von RUSSELL beobachtete langsame
Kleinerwerden der solitären Welle interpretierte AIRY dahingehend und faßte es
als Bestätigung seiner Theorie auf.
AIRY hatte auch das Brechen von Wellen am Strand beschrieben
und war davon ausgegangen, daß ein Aufsteilen der Wellen dadurch stattfand,
daß die in der Welle oberen Wassermoleküle schneller in Richtung der
Wellenbewegung geworfen wurden als die in der Welle unteren. Schon 1807 war eine
ähnlicher Erklärung von YOUNG vorgeschlagen worden [Young 1807]. Nach der
Gleichung von LAGRANGE (Gleichung 2.1), wenn für H die Höhe des
Wassermoleküls über dem Meeresgrund angenommen wird, so erläuterte er, hat
die Spitze der Welle eine höhere Geschwindigkeit als die Ränder, so daß die
Welle sich aufsteilt und schließlich bricht. Es gelang jedoch im letzten
Jahrhundert noch nicht, durch den Effekt des Aufsteilens der Welle die scheinbar
unüberwindliche Dispersion einer Summe oszillatorischer Wellen in der
Vorstellung auszugleichen und so eine solitäre Welle vorstellbar zu machen.
In seiner Arbeit von 1844 machte RUSSELL deutlich, daß die
von ihm gefundene solitäre Welle nicht zu AIRYs Theorie paßte. Er hob hervor,
daß er die davon abweichenden Eigenschaften besonders genau überprüft hatte
und seine früheren Resultate nur bestätigen konnte:
* Die Geschwindigkeit c der solitären Welle ist
gegeben durch c2= g(H+h).
* Ihre Amplitude braucht nicht klein zu sein.
* Im künstlichen Kanal ist die Abnahme der Amplitude der
Welle so gering, daß sie nicht als Auseinanderlaufen der Welle angesehen
werden kann. In Schiffskanälen hängt das Kleinerwerden der Welle signifikant
von der Struktur der Kanalränder ab. Das sah RUSSELL als ein deutliches Indiz
für Reibungsverluste an.
* Die negative solitäre Welle verhält sich nicht wie die
positive, sondern zieht oszillatorische Wellen hinter sich her und dissipiert
recht schnell (s. Abb. 2.7).
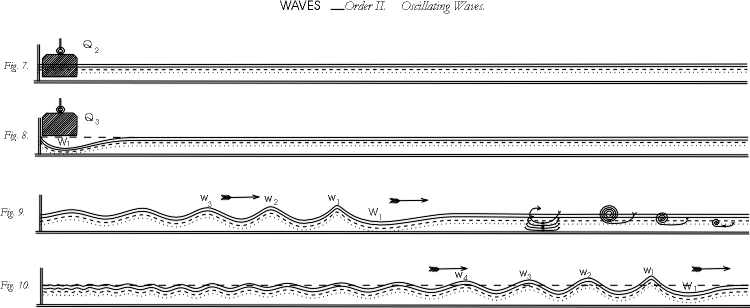
Abbildung 2.7:
Zeichnung aus [Russell 1844]. Die Erzeugung einer negativen
Welle (Fig.7, 8). Sie zieht, so RUSSELL, immer oszillatorische Wellen hinter
sich her (Fig. 9,10). In Fig. 9 sind die Bewegungen der Wassermoleküle
dargestellt.
Das wichtigste, auch mathematisch am besten greifbare
Kriterium zur Zurückweisung von AIRYs Kritik betraf die Geschwindigkeit der
Welle. Daher wandte RUSSELL besondere Mühe darauf an, die Geschwindigkeit durch
besonders viele und genaue Messungen, die er in Grafiken darstellte, über allen
Zweifel erhaben zu machen. Sein besonderes experimentelles Geschick, mit
einfachen Mitteln zu optimalen Ergebnissen zu kommen, kann etwa daran ersehen
werden, wie er die Geschwindigkeit der solitären Welle vermaß: Er ließ die
Welle erst eine Strecke von einigen Metern durch das lange Becken laufen, damit
sich anfängliche Störungen, die bei der Erzeugung der Welle auftraten,
verliefen. Da die Welle immer wieder an den Beckenenden reflektiert wurde, ließ
er sie für eine Meßreihe oft, bei größeren Wellen über hundert Mal, durch
das Becken laufen. Bei jedem Durchlauf durch das Becken passierte die Welle
einen oder mehrere Beobachterstationen, wo jedes Mal die Zeit genommen wurde.
Damit wurde auch die Verringerung der Geschwindigkeit aufgrund der Abnahme der
Wellenhöhe gemessen. Der Beobachter fokussierte durch eine Blende das auf der
Wasseroberfläche sichtbare Spiegelbild einer hoch über dem Becken angebrachten
Kerze. Jede Bewegung der Wasseroberfläche verursachte so eine starke Bewegung
des Reflexes der Kerze für den Beobachter. Auf diese Weise konnte der Durchgang
eines Wellenscheitels einer sogar ohne Hilfsmittel nicht mehr erkennbaren Welle
mit einer Höhe unter einem Millimeter mit großer Genauigkeit gestoppt werden
[Russell 1837b].
Nachdem RUSSELL auf diese Weise AIRYs Kritik zurückweisen
konnte, waren wesentliche Fragen zur Theorie der solitären Welle weiterhin
offen. Lediglich die Atmosphäre, in der diskutiert wurde, war nun angespannt
[Emerson 1977]. RUSSELL zog sich aus dieser Diskussion zurück. Unabhängig von
der später weiterhin auftretenden Kritik lehrte er seine Einsichten als
Antworten auf manche offenen Fragen des Schiffbaus [Russell 1865].
Die Diskussion um RUSSELLs solitäre Welle ging jedoch
unvermindert weiter. Im Jahre 1845 wählte der englische Mathematiker S. EARNSHAW
den Ansatz u = u(x-ct), um die solitäre Welle zu beschreiben.
RUSSELL hatte beobachtet, daß ein senkrecht im Wasser hängender Faden beim
Passieren einer solitären Welle senkrecht blieb; er hatte daher u(x)
unabhängig von z angenommen. EARNSHAW schienen die Unveränderlichkeit
der Wellenform und die Annahme u unabhängig von z abgesicherte
experimentellen Fakten zu sein, die als Grundlage eines mathematischen Ansatzes
dienen konnten [Earnshaw 1849]. Mit der Beobachtung u = u(x-ct) und der
Vorstellung einer diskontinuierlichen Funktion für die Form der solitären
Welle hatte RUSSELL unbewußt eine Falle ausgelegt, die erst Lord RAYLEIGH 1876
zu erkennen imstande war [Rayleigh 1876]: u = u(x) kann die
Laplace-Gleichung (2.8) nicht erfüllen, also ist eine solche Bewegung nicht
wirbelfrei. Mit einer von einem Geschwindigkeitspotential ausgehenden
Bewegungsgleichung kann die Rotation nicht beeinflußt werden, sie bleibt
konstant. Da das ruhende Wasser vor und hinter der Welle jedoch wirbelfrei ist,
muß mit u = u(x) eine Diskontinuität vor und hinter der Welle
auftreteten. Damit waren die Bedingungen u = u(x-ct) und η = diskontinuierliche
Funktion konsistent und schienen sich gegenseitig zu rechtfertigen. In diese
Falle tappte nun auch EARNSHAW, der nach einigen Rechnungen zu einer etwas
unübersichtlichen Form der solitären Welle kam:
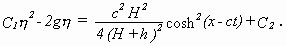
Diese Formel veranlaßte EARNSHAW zu der grotesk
erscheinenden Anschauung, die Welle als abgeschnittenen, umgedrehten cosh2-Bogen
inmitten des ansonsten ruhenden Wassers zu betrachten.
Bei diesem Stand der Diskussion meldete sich eine weitere
Größe unter den englischen Naturwissenschaftlern zu dem Thema zu Wort. GEORGE
GABRIEL STOKES (1819-1903) verfasste einen Review-Artikel [Stokes 1846], in dem
er die bekannten Ergebnisse der Theorie der Wasserwellen kurz zusammenfasste.
Auch RUSSELLs Ergebnisse streifte STOKES, jedoch in einer irreführenden Weise,
da er versuchte, die Theorie der solitären Welle in die der langen Wellen
einzubinden. Es scheint, als ob STOKES diese Einbindung als die einzige
Möglichkeit ansah, die solitäre Welle theoretisch zu beschreiben. Denn obwohl
er andere Lösungsansätze suchte - die auf Diskontinuitäten führenden
Lösungsansätze AIRYs und EARNSHAWs wies er als unakzeptabel zurück - kam
STOKES immer wieder auf die Degradierung der Wellenhöhe zurück, die er als
Dispersion zu interpretieren suchte. Auch gab STOKES an, daß die Ergebnisse der
Russellschen Experimente die Geschwindigkeitsbeziehung für lange Wellen c =
(gH)1/2 bestätigten. Diese für vernachlässigbare Wellenhöhe ja
zutreffende Bemerkung verdeckte ganz den außergewöhnlichen Charakter der
solitären Welle. Obwohl STOKES Zusammenfassung belegt, daß er RUSSELLs
Ergebnisse gut studiert haben muß, scheint er die Besonderheiten der solitären
Welle schlicht nicht akzeptiert zu haben. In diesem Sinne schloß er den
Abschnitt zur solitären Wellen, indem er bemerkte [Stokes 1846, S. 9]:
"It is the opinion of Mr. Russell that the solitary
wave is a phenomenon sui generis in nowise deriving its character from
the circumstances of the generation of the wave. His experiments seem to
render this conclusion probable. Should it be correct the analytical character
of the solitary wave remains to be discovered".
Es scheint hier zunächst, daß STOKES die Suche nach einer
eigenständigen Theorie für die solitäre Welle noch nicht aufgegeben hatte.
Die direkt anschließende Bemerkung offenbart jedoch, daß er sich recht sicher
damit war, daß die solitäre Welle in die Theorie der langen Wellen einzuordnen
sei:
"A complete theory of this wave should give, not only
the velocity of propagation, but also the law of its degradation, at least of
that part of degradation which is independent of friction, which is probably
the greater part. With respect to the importance of this peculiar wave however,
it must be remarked that the term solitary wave as so defined, must not
be extended to the tide wave, which is nothing more (as far as regards the
laws of its propagation) than a very long wave of which the form may be
arbitrary."
Hiermit zeigte STOKES seine ganze Ablehnung gegenüber
RUSSELLs Theorie. Denn zum einen verliert eine dispersive solitäre Welle
gänzlich ihren besonderen Charakter und zum anderen beschrieb RUSSELL den
Charakter der Gezeitenwelle nicht mit ihrer Geschwindigkeit, die genau mit der
Theorie der langen Wellen übereinstimmt, sondern mit ihrer Dispersionsfreiheit
gepaart mit dem einzelnen Auftreten.
Ein Jahr später bekräftigte STOKES seine Ablehnung der
Besonderheiten der solitären Wellen in einer Abhandlung über oszillatorische
Wellen [Stokes 1847]. Es erscheint zuerst widersinnig, die solitäre Welle in
einer Arbeit über oszillatorische Wellen behandeln zu wollen, doch STOKES
zeigte sich im Verlaufe dieser Arbeit sicher, daß die solitäre Welle mit
oszillatorischen Wellen beschreibbar sei. Obwohl er damit in die Irre ging, ist
sein Beitrag dennoch in zweifacher Hinsicht erwähnenswert: STOKES Ansatz führt
ein Stück weit in die Richtung der cnoidalen Wellen, die auch periodisch
sind, jedoch für λ ®
¥ in die sech2-Form der
Ein-Solitonenlösung der KdV-Gleichung übergehen. Außerdem wird die Arbeit als
der historische Beginn des Studiums nichtlinearer Wellen bezeichnet [Dea., Dal.
1984], [Whitham 1974]. STOKES war bestrebt, eine möglichst allgemeingültige
Lösung zu erhalten. Daher versuchte er, die in den grundlegenden Gleichungen
auftretenden nichtlinearen Terme soweit wie möglich zu berücksichtigen. Sein
Ansatz beruht darauf, ebene, formstabile Wellen zu betrachten, bei denen für
das Geschwindigkeitspotential φ gilt
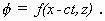
Damit kann in der Bernoulli-Gleichung
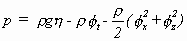
(2.4)
die Zeitabhängigkeit eliminiert werden und es bleibt
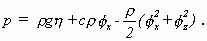
(2.5)
Weiter setzte STOKES als Randbedingung, daß die freie
Oberfläche der Flüssigkeit während der Wellenbewegung als solche erhalten
bleibt. Für die Beschreibung dieses Umstands wählte STOKES als Variable nicht
die Oberfläche η, was ihn zu der heute
üblichen Gleichung (2.14) geführt hätte, sondern p(x,z) an der Stelle p = 0.
Dies führt zu der Gleichung
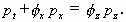 (2.6)
(2.6)
Der Druck p aus Gleichung (2.5) und pt = -c px
in Gleichung (2.6) eingesetzt liefert
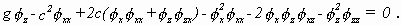 (2.7)
(2.7)
Diese, bis hierher noch exakte, Gleichung diente STOKES als
Ausgangspunkt für seine weiteren Rechnungen. Hierbei beschränkte er sich
nicht, wie damals üblich, nur auf die einfachsten Terme, sondern
berücksichtigte auch die in φ
quadratischen Terme in der Klammer von Gleichung (2.7). STOKES hier folgende,
längere Rechnungen werden in [Bullough 1988] diskutiert und es bleibt hier, auf
die Ergebnisse und STOKES Folgerungen einzugehen. Aus der Laplace-Gleichung, die
aus der von STOKES angenommenen Inkompressibilität und Wirbelfreiheit des
Wassers folgt
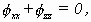 (2.8)
(2.8)
bestimmte er das Geschwindigkeitspotential φ.
Hierbei legte er periodische Randbedingungen fest und suchte die allgemeine
Lösung für φ durch Bedingungen
einzuschränken. Er entwickelte φ in eine
Reihe, deren Konvergenz von verschiedenen Kriterien abhing. Das Ergebnis für φ
wiederum eingesetzt in die Bernoulli-Gleichung (2.5) für die freie
Wasseroberfläche lieferte ihm eine Lösung für η.
In einer ersten Näherung gelangte Stokes auf diesem Wege zu
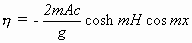 (2.9)
(2.9)
mit m = 2π/λ
und A = Konstante. Die von STOKES für diese Näherung gefundene
Wellengeschwindigkeit
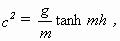 (2.10)
(2.10)
entspricht AIRYs Resultat (2.3) für lange Flachwasserwellen.
In einer zweiten Näherung setzte STOKES sein erstes Resultat für φ
in die quadratischen Terme der Gleichung (2.7) ein. Mit dieser Gleichung kam er
zu der Form der Wasseroberfläche
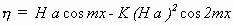
mit a, K = Konstanten. Diese Gleichung stellt für
kleine mH die ersten zwei Terme der Fourierentwicklung der cn2-Funktion
dar, worauf KORTEWEG und de VRIES 1895 hinwiesen. Stokes hatte allerdings
periodische Randbedingungen angenommen, und konnte somit von cn2
nicht zu sech2 kommen.
Die periodische Form der Wellenbewegung wurde von STOKES
unter den angenommenen Randbedingungen für die einzig mögliche Bewegung
gehalten. Das brachte ihn dazu, einen Kommentar zu RUSSELLs Arbeiten anzufügen.
Er bemerkte, wie auch schon AIRY vor ihm, daß eine Form wie Gleichung (2.9)
keine gleichförmig bewegte und gleichzeitig solitäre Welle hervorbringen kann.
Die von RUSSELL beobachtete Abnahme der solitären Welle sah er deshalb wie AIRY
als für diese charakteristisch an. STOKES Argumentation enthält jedoch zwei
Fehler. Zum einen war er wie AIRY in seinem Ansatz für φ
als Lösung der Laplace-Gleichung von oszillatorischen Wellen ausgegangen. Das
schien ihm von vorn herein unausweichlich zu sein. Zum anderen war er von sehr
langen Wellen und später sogar von λ » H
ausgegangen, was für solitäre Wellen nicht zutreffen muß. Die solitäre Welle
betrachtend, bemerkte er dazu, daß seine Näherung für sehr kleine solitäre
Wellen gelte. Und wenn diese somit der Gleichung (2.9) folgten, so müßten es
auch die großen solitären Wellen tun, die sich damit nicht unverändert
bewegen könnten. Auf den Fehler dieses Gedankengangs kam STOKES etwa 1880 [Stokes
1891]: Kleine solitäre Wellen konnten eben auch mit sehr langen Wellen der Form
(2.9) angenähert werden, die nur sehr wenig dispersiv sind. Für große
solitäre Wellen gilt dies jedoch nicht.
Vielleicht war STOKES mit seiner "Lösung" des
Russellschen Problems selber nicht zufrieden. Denn zwei Jahre später versuchte
STOKES mit einem völlig anderen Ansatz zu einer der solitären Welle
nahekommenden mathematischen Beschreibung zu gelangen [Stokes 1849]. RUSSELLs
Beobachtung des senkrecht im Wasser hängenbleibenden Fadens beim Passsieren
einer solitären Welle griff STOKES auf und setzte wie EARNSHAW explizit u = u(x).
Diese Näherung führt jedoch wieder zu der Geschwindigkeit der Welle von
LAGRANGE (2.1). STOKES schien sich in einem Zwiespalt zu befinden. Einerseits
legt die Weise, wie er RUSSELL zitierte und einige seiner Ergebnisse verwendete,
um eigene Rechnungen auf ihnen aufzubauen oder eigene Ergebnisse zu bestätigen,
nahe, daß er RUSSELLs Bericht von 1844 schätzte. Andererseits konnte er mit
seinen, ihm allgemein scheinenden Ergebnissen die solitäre Welle nicht
erklären. Ein Grund hierfür, die Näherung durch lange Wellen, schien ihm
bewußt zu sein, wie der Abschluß seiner Betrachtung zeigt [Stokes 1849, S.
228]:
"...in the case of a solitary wave artificially
excited in a canal ... it appears to be necessary to take account of the
finite length, as well as finite hight of the wave."
Es scheint, als ob STOKES das Problem der solitären Welle
über Jahrzehnte nicht vergessen konnte. Denn er kam etwa 1880, also etwa 34
Jahre nach seiner ersten Arbeit zur solitären Welle, beim Nachdenken über
Wellen auf seinen oben beschriebenen zweiten Fehler [Stokes 1891]. Als er LORD
RAYLEIGH auf das Problem ansprach, machte dieser ihn auf seine eigene Arbeit zu
solitären Wellen aufmerksam [Rayleigh 1876], womit nun STOKES wußte, daß es
solitäre Wellen geben konnte. Seinen ersten Fehler hatte STOKES zu diesem
Zeitpunkt noch nicht erkannt und versuchte, mit einer "trial-and-error-Methode"
den Umständen der solitären Welle auf die Spur zu kommen [Stokes 1883, 1891].
Weitere Versuche, mit dem Earnshawschen Ansatz zu einer
Beschreibung der solitären Welle zu gelangen, unternahm ANDREW ROBERTSON
[Robertson 1850, 1851, 1852], der zu einer der Russellschen Angabe in der Form
ähnlichen Wellengeschwindigkeit gelangte, nämlich
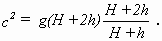
Bei der mathematischen Beschreibung physikalischer Phänomene
hingen die britischen Naturwissenschaftler stark an ihren Vorstellungen über
die Dinge [Cros., Smith 1978]. Dienten diese als Grundlage für mathematische
Ansätze, so konnten Fehler in den Annahmen zu mathematischen Schwierigkeiten
führen: RUSSELL wie AIRY hatten a priori angenommen, daß eine Welle mit einer
Sinusfunktion verknüpft sein müsse und waren damit in die Irre gelaufen.
Ebenso hartnäckig hielt sich die Vorstellung von der diskontinuierlichen
Funktion für die solitäre Welle, der u.a. RUSSELL, AIRY und EARNSHAW anhingen.
Erst durch die Assimilation französischer analytischer Techniken konnte sich
die britische Mathematische Physik von diesem Denkansatz lösen und
weiterentwickeln [Wise 1981]. Doch dieser Vorgang war langwierig.
Im deutschsprachigen Raum wurde in diesen Jahrzehnten so gut
wie gar nicht auf die Entdeckung der solitären Welle eingegangen. Lediglich
GOTTHILF HAGEN (1797 - 1884), der in einer Abhandlung "Über Wellen auf
Gewässern von gleichmäßiger Tiefe" [Hagen 1861] oszillatorische Wellen
untersuchte, verglich RUSSELLs Ergebnisse mit seinen eigenen. Da HAGEN jedoch a
priori davon ausging, daß es einzelne Wellen ohne nachfolgende oszillatorische
Wellen nicht geben konnte, stellte er die Zuverlässigkeit von RUSSELLs
Forschungen in Abrede. HAGENs Urteil über RUSSELLs Arbeit fiel vernichtend aus:
Die Abweichungen in den Eigenschaften der solitären Welle im Vergleich zu
oszillatorischen Wellen begründete HAGEN mit Fehlern und Unzuverlässigkeiten
in RUSSELLs Arbeiten. Auch die von der Wellenamplitude abhängige
Wellengeschwindigkeit zweifelte HAGEN an und kritisierte Einzelheiten an der
Russellschen Meßapparatur.
In Frankreich wurden die britischen Forschungsergebnisse zur
solitären Wasserwelle sehr schnell aufgenommen und diskutiert. Über seine
Arbeiten hatte RUSSELL im Jahre 1837 je einen ausführlichen Bericht in England
[Russell 1837b] und Schottland [Russell 1840a] vorgelegt. Der schottische
Bericht wurde zwar erst 1840 gedruckt, war jedoch schon 1837 als Bericht von
einem Korrespondenten der "Annales des Ponts et Chaussées" nach
Frankreich gebracht worden. Dieser Bericht wurde noch im selben Jahr übersetzt
und mit allen Tabellen und Zeichungen in den Annales abgedruckt [Russell 1837c].
Denn in Frankreich hatte man auch schon das Phänomen der abnehmenden Reibung
bei höheren Geschwindigkeiten bei Kanalbooten beobachtet und maß daher
RUSSELLs Forschungen große Bedeutung zu [Russell 1837c, S. 143 Fußnote].
Die erste Reaktion auf diesen Artikel in den "Annales"
kam von ANATOLE DE CALIGNY (1811 - 1892), der sich mit Wasserhebern beschäftigt
hatte und eigene Erfahrungen in RUSSELLs Experimenten wiederfand. Doch die Art,
mit der er ab 1842 mit recht vielen kleinen Veröffentlichungen zu
Wellenbewegungen die französische Wissenschaft in die Ergebnisse seiner
Experimente zur solitären Welle einzuführen versuchte, taugte mehr zur
Verwirrung als zur Erklärung des Phänomens [Caligny 1842-72, 1843, 1844, 1848,
1866]. In seiner Arbeit von 1844 z.B. trennte CALIGNY die solitäre Welle in
zwei unabhängige Phänomene: Als onde solitaire bezeichnete er
die Welle, die durch Hinzufügen einer Menge Wassers an einem Ende des
Versuchsbeckens entsteht und dann unverändert duch das Becken läuft. Als onde
de translation hingegen bezeichnete er die sich vor einem gezogenen Kahn
ausbildende Welle. Damit stieß er in das gleiche Horn wie AIRY - wahrscheinlich
ohne dessen Arbeit [Airy 1845] zu kennen - der behauptet hatte, daß nur eine
äußere Kraft wie z.B. ein Kahn eine einzelne und unveränderte Welle aufrecht
erhalten konnte. CALIGNY schilderte eigene Versuche mit der onde de
translation, die Zweifel an den Gesetzen der onde solitaire aufkommen
ließen, so CALIGNY. Durch dieses Vermischen der Phänomene kämen in der
englischen Literatur die Meinungsverschiedenheiten über die Geschwindigkeit der
Wellen zustande. CALIGNY versicherte aus eigenen Versuchen, daß für eine onde
solitaire c2 = gH gilt. Bei der onde de
translation hingegen sei c auch von dem sie erzeugenden Boot oder
sonstigen Gegenstand abhängig. Je größer der Gegenstand sei, desto schneller
sei die Welle. Damit widersprach er RUSSELLs Aussagen direkt. Daß der die Welle
erzeugende Gegenstand Einfluß auf die Wellenhöhe hat und diese wiederum auf
die Wellengeschwindigkeit, scheint CALIGNY nicht bemerkt zu haben. Auch in
seinen späteren Arbeiten zur solitären Welle schaffte CALIGNY nicht wesentlich
mehr Klarheit, wenngleich er auch nun die solitäre Welle und Translationswelle
als ein Phänomen ansah. Immer wieder zitierte er RUSSELL und brachte
eigene Beobachtungen mit dessen Ergebnissen in Verbindung. Doch da er u.a. die
Bewegung der Wassermoleküle innerhalb der solitären Welle mit deren Bewegung
in oszillatorischen Flachwasserwellen verglich, kam er zu einigen
Widersprüchen. CALIGNY machte qualitative Beobachtungen und so gut wie keine
Messungen. Daher konnte er nie mit der Genauigkeit der Russellschen Studien
konkurrieren, die er zitierte. Seine Arbeiten können eher als ein
Aufmerksammachen auf die solitäre Welle und auf RUSSELLs Arbeiten in Frankreich
gewertet werden.
Wesentlich genauer ging HENRI EMILE BAZIN (1829-1917) auf
RUSSELLs Experimente ein [Bazin 1852, 1865]. Im Jahre 1859 machte er eigene
Experimente zur solitären Welle in einem Teilstück des Canal du Bourgogne bei
Dijon sowie in einem flachen, langen Graben daneben. In beiden Gewässern
erzeugte er durch Hinzufügen einer größeren Menge Wasser aus Schleusen eine
positive solitäre Welle und durch Entfernen einer Menge Wasser durch eine
Schleuse eine negative solitäre Welle. Die Ergebnisse seiner Versuche stimmen
bis auf ihre wesentlich geringere Genauigkeit mit denen von RUSSELL überein.
Daher anerkannte BAZIN ohne Umschweife RUSSELLs Arbeiten und bezeichnete ihn als
einen befähigten Experimentator. BAZIN führte seit 1855 Studien zum Fluß von
Wasser in Röhren und Kanälen von HENRY PHILIBERT GASPARD DARCY (1803-1858)
fort und sein Forschungsschwerpunkt war die Reibung von strömenden Gewässern [Rouse,
Ince 1857]. Die Untersuchung von Wellen in Kanälen mit und ohne Strömung,
insbesondere der solitären Welle und der Flutwelle, bildete nur ein Nebengebiet
seiner Forschungen. Neue wesentliche Erkenntnisse über die solitäre Welle
vermochte BAZIN mit seinen Experimenten nicht zu gewinnen und an einem
theoretischen Erklärungsansatz seiner Ergebnisse mangelte es ganz, so daß
BAZINSs Versuche als eine Bestätigung der Russellschen experimentellen Arbeiten
gesehen werden können.
Weiter mit Kapitel 2.3: Mathematische
Beschreibungen der solitären Welle
[Inhaltsverzeichnis]
![]()

