5.2 Von numerischen Simulationen zur inversen Streumethode
Das folgende Zitat aus [Ford 1992, S. 273] beschreibt den Beginn einer Entwicklungslinie, aus deren Anfängen, ähnlich den Anfängen der Entwicklungslinien in der Differentialgeometrie und der Festkörperphysik, schwer zu sehen ist, wie sie mit der Solitonentheorie zusammengehören könnte. Die Entwicklungslinie begann mit numerischen Experimenten am zu der Zeit leistungsstärksten Computer der Welt: MANIAC-I.
"In the early 1950s MANIAC-I had just been completed and sat poised for an attack on significant problems. On one of his several visits to the Los Alamos Scientific Laboratory during this period, Enrico Fermi joined mathematician Stan Ulam and computer scientist John Pasta in a quest for suitable problems. They each recognized that MANIAC-I could answer questions holding great interest for mathematics and physics, but which one deserve immediate attention? After reflecting on the matter, Fermi suggested that it would be highly instructive to integrate the equations of motion numerically for a judiciously chosen, one-dimensional, harmonic chain of mass points weakly perturbed by nonlinear forces. ... the initial studies were intended merely to test the simplest and most widely believed assertion of equilibrium statistical mechanics such as equipartition of energy, ergodicity, and the like."
Die Motivation für die numerischen Experimente können in der von DEBYE aufgestellten Frage gesucht werden, warum Festkörper endliche Wärmeleitfähigkeit haben. DEBYE selbst hatte vorgeschlagen, die Antwort auf seine Frage in der nichtlinearen Kopplung der Atome innerhalb des Kristallgitters zu suchen, die eine Energiedissipation verursacht. Das hatte FERMI angeregt, numerische Experimente zur nichtlinearen Kopplung im Festkörper vorzunehmen [Fokas 1991]. Die Erinnerungen von ULAM [Ulam 1965] an die Anfänge jener numerischen Experimente weisen darauf hin, daß FERMI ganz bewußt innerhalb der Mathematischen Physik einen Vorstoß in das Gebiet der nichtlinearen Systeme unternehmen wollte:
"Fermi expressed often a belief that future fundamental theories in physics may involve non-linear operators and equations, and that it would be useful to attempt practice in the mathematics needed for the understanding of non-linear systems. The plan was to start with the simplest such physical model and to study the results of the calculation of its long time behaviour. ... We had planned the work in summer of 1952 and performed the calculation in the following summer."
Als Untersuchungsobjekt wurde das numerische Modell einer linearen Kette aus 64 Massepunkten gewählt, die nichtlinear miteinander gekoppelt sind. Die Ergebnisse dieser numerischen Experimente, die u.a. in [Ford 1992], [Newell 1985] und [Jackson 1990] zusammengefaßt und erläutert sind, bezeichnete FERMI als "little discovery". Es hatte sich nämlich überraschenderweise gezeigt, daß trotz nichtlinearer Kopplung der Massenpunkte die Anfangsenergie sich nicht auf alle möglichen Moden verteilte, sondern nur auf einige erste Moden und daß sich ca. 97% der Anfangsenergie nach geringer Zeit wieder in der ersten Mode sammelte.

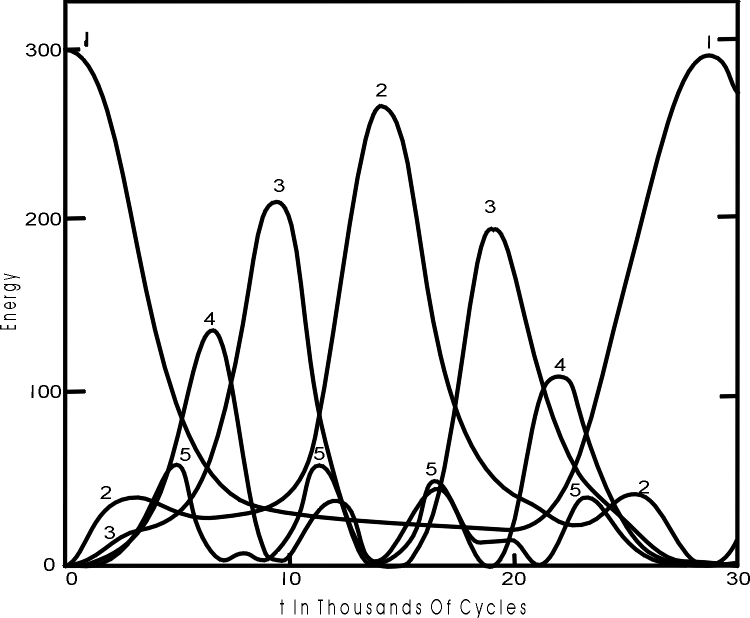
Abbildung 5.1:
Aus [FPU 1955] entnommene Grafik der Energieverteilung auf die verschiedenen Moden im Verlaufe der Zeit. Die Anfangsstellung der Massepunkte war in Ruhe in einer halben Sinuswelle. Sofort nach Beginn des Schwingens der Massepunktreihe absorbieren die untersten Moden Energie. Nach etwa 157 Perioden (nicht zu verwechseln mit den in der Ordinate angegebenen Rechenzyklen des Computers) sammelte sich die Anfangsenergie fast vollständig wieder in der Ursprungsmode ("FPU-Wiederkehr").
Diese Ergebnisse schienen der statistischen Mechanik zu widersprechen, die bei nichtlinearen Systemen eine Gleichverteilung der Energie in allen Freiheitsgraden voraussagte. Im Mai 1955 erschienen die Ergebnisse der numerischen Experimente in einem Preprint [FPU 1955]. Im November 1954 war FERMI verstorben. Die Veröffentlichung des Preprints scheiterte an dem Umstand, daß sie ohne FERMIs Namen nicht geschehen konnte, mit FERMIs Namen wollten PASTA und ULAM das Preprint jedoch auch nicht veröffentlichen, da FERMI es nie gesehen und damit nicht gutgeheißen hatte [Ford 1992]. Das Preprint wurde jedoch auf Tagungen und Treffen von ULAM vorgestellt und erfuhr so, nicht zuletzt wegen seiner erstaunlichen Ergebnisse, eine weite Verbreitung. Erstaunen, aber auch Ablehnung und Kritik an der Versuchsdurchführung waren die Reaktionen, denn trotz vielfacher Bemühungen konnten die Ergebnisse zuerst nicht erklärt werden. Ein störungstheoretischer Lösungsansatz von JACKSON [Jackson 1963] zeigte, daß das FPU-System nicht weit entfernt von einem integrablen System sein konnte [Ford 1992]. Daß das FPU-System tatsächlich durch ein integrables System angenähert werden konnte, zeigten dann 1965 MARTIN KRUSKAL und NORMAN ZABUSKY in [Zab., Kru 1965]. Da die Energie des FPU-Systems in den untersten Moden blieb, motivierte FERMIs Ansatz
![]() (5.1)
(5.1)
einen Übergang von Auslenkungen qn diskreter Teilchen zu kontinuierlichen Auslenkungen q(x). Dieser führte nach einiger Rechnung zur KdV-Gleichung
![]() (5.2)
(5.2)
KRUSKAL war schon im Winter 1953-54 von ULAM in Los Alamos von dem FPU-Pänomen unterrichtet worden [Kruskal 1978]; auch ZABUSKY hatte sich schon einige Jahre mit dem FPU-Phänomen beschäftigt und dazu veröffentlicht [Ulam 1965], [Ford 1992]. KRUSKAL vermutete einen Zusammenhang von Gleichung (5.1) mit der aus der Plasmaphysik bekannten KdV-Gleichung und er suchte danach. ZABUSKY berichtete [persönliche Mitteilungen], wie sie 1964 beide oft im Wohnzimmer von ZABUSKYs Haus an der Tafel an der Lösung des FPU-Phänomens arbeiteten und KRUSKAL versuchte, das FPU-Problem so anzunähern, daß eben die KdV-Gleichung als Kontinuum-Limit herauskam. Das gelang ihm schließlich auch.
Hier ist ein kurzer Einschub am Platze. Schon 1960 war die KdV-Gleichung im Zusammenhang mit der Plasmaphysik aufgetaucht (s. Kap. 5.1). KRUSKAL, der schon seit 1951 auf dem Feld der Plasmaphysik forschte (s. Kurzbiographie), hätte 1964 die KdV-Gleichung und auch ihr Zusammenhang mit der Plasmaphysik bekannt sein können. ZABUSKYs Bemerkung, daß KRUSKAL nach dem Zusammenhang zwischen dem FPU-Problem und der KdV-Gleichung suchte, weist darauf hin. Daß die KdV-Gleichung Mitte der 60er Jahre innerhalb der Plasmaphysik schon recht bekannt gemacht worden war, wurde in Kapitel 5.1 dargestellt. KRUSKAL selbst beschrieb jedoch im Zusammenhang mit seiner Wiederentdeckung der Gleichung von KORTEWEG und de VRIES [Kruskal 1995, S. 132]:
"To bring out the point how little attention was paid to their equation, let me mention that after I derived it on my own and only then discovered it to be a `known´ and named equation, I asked one of the greatest analysts of the time, Solomon Bochner, a Princeton mathematics professor, what he could tell me about it. The answer was, nothing. I do not recall now whether he had even ever heard of it, but it was clear that he had never thought about it."
Da die KdV-Gleichung relativ einfach aussieht, strebten KRUSKAL und ZABUSKY ihre Integration an. Sie versuchten es numerisch. Und diese numerische Integration der KdV-Gleichung führte sie zu nicht minderen Überraschungen als es FERMIs "little discovery" selbst war. Unter periodischen Randbedingungen führte eine cosinus-Periode als Anfangsbedingung zu einem Aufbrechen des cosinus-Bogens in acht Wellenberge, deren Fortpflanzungsgeschwindigkeit von der Amplitude abhing. Diese Wellenberge durchdrangen sich zwar, wie es die Nichtlinearität der KdV-Gleichung verlangte, sie verließen den Kollisionsort allerdings völlig ungestört. Ferner überlagerten sich alle Wellen nach einer Weile wieder fast zu ihrem Ausgangszustand, der Kosinusfunktion.
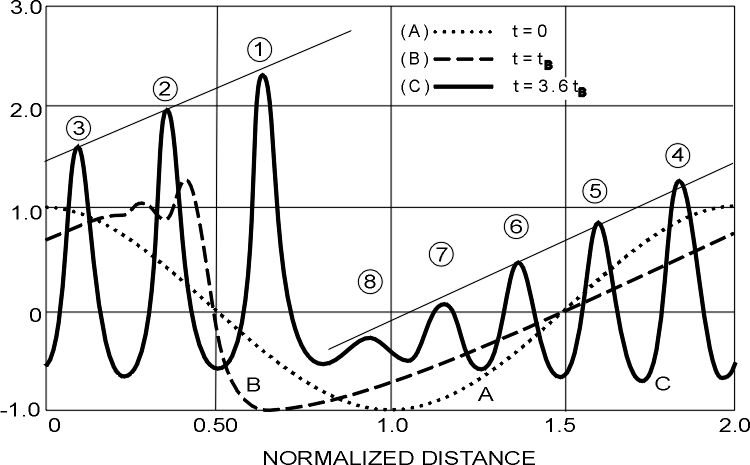
Abbildung 5.2:
Die numerisch integrierte Lösung der KdV-Gleichung von KRUSKAL und ZABUSKY; aus [Zab., Kru 1965]. Die gepunktete Linie bezeichnet den Anfangszustand, die gestrichelte die Entwicklung nach einer gewissen Zeit und die durchgezogene zu einem noch späteren Zeitpunkt. Die Wellengeschwindigkeit ist proportional zur Wellenhöhe, d.h. die großen Wellen "überholen" die kleinen.
Zur Verdeutlichung der außergewöhnlichen Kollisionseigenschaften bannten KRUSKAL und ZABUSKY ihre numerischen Ergebnisse auf Zelluloid, indem sie den Bildschirm abfilmten. So konnten ihre Ergebnisse eindrucksvoll dargestellt werden. ZABUSKY bemerkte hierzu [Zabusky 1995, S. 159]:
"Our numerical simulation results were visualized by Gary Deem and myself in a cinema, the first for a nonlinear partial differential equation [DKZ 1965]. ... This work came about through the effective collaboration of Kruskal (asymptotologist) at the Princeton Plasma Physics Laboratory and Deem (computationalist) and myself (`visiometricist´) at Bell Telephone Laboratories in Whippany, New Jersey."
Nach der vielbeachteten numerisch-experimentellen Entdeckung der Solitonen durch KRUSKAL und ZABUSKY beschleunigte sich der Takt der Entdeckungen innerhalb der Entwicklungslinie erheblich. Nun war allerdings nicht mehr FERMIs "little discovery" das Forschungsobjekt, sondern die von KRUSKAL und ZABUSKY so getauften Solitonen [Zab., Kru. 1965] und die KdV-Gleichung. Es stellte sich die Frage, ob die KdV-Gleichung integrabel in irgendeinem Sinne sei. Der Zusammenhang der KdV-Gleichung mit der Gasdynamik brachte KRUSKAL und ZABUSKY darauf, daß Erhaltungssätze der Form Tt + Xx = 0 in dieser Frage eine Antwort geben könnten. Hierbei stellt T die erhaltene Dichte dar und -X den dazugehörigen Fluß. Erhaltungssätze "verhindern Chaos" und erlauben z.B. durch Schockwellen hindurchrechnen zu können [Newell 1985]. Die ersten beiden - für Masse und Impuls und für die Energie - waren bekannt. WHITHAM hatte einen dritten gefunden, der Boussinesqs Stabilitätsmoment (siehe [Artikel I]) entsprach. KRUSKAL und ZABUSKY fanden weitere Erhaltungssätze. Diesen Prozess beschreiben MIURA [Miura 1976] und Newell [Newell 1985, S. 9]. Letzterer sei zitiert:
"The next surge of momentum came with the arrival of Robert Miura who was asked by Kruskal to get his feet wet by searching for a conservation law at level seven. He found one and then quickly filled in the missing level six. Eight and nine fell quickly and Kruskal and Miura were certain that there was an infinite number. However, rumours originated from the Courant Institute that nine was the limit. ... Miura was therefore challenged to find the tenth. He did during a two week vacation in Canada in the summer of 1966. (There is also a rumour that he was seen about this time in Mt. Sinai, carrying all ten.)"
Bald wurde von KRUSKAL und MIURA, und von GARDNER gleichzeitig der Beweis für die Existenz unendlich vieler Erhaltungssätze erbracht [Miura 1976, S. 422]:
"While working late at afternoon, Martin Kruskal and the author found a proof for the existence of an infinite number of conservation laws using the WKB formalism. As we examined our result, Clifford Gardner called from his home and told us he had just obtained an existence proof - a different one!"
Die vielen Erhaltungssätze machten nun allerdings die Geschichte unübersichtlich und wurden an diesem Punkt nicht weiter verfolgt. Es war vielmehr wieder MIURA, der neuen Schwung mit der Entdeckung der modifizierten Korteweg-de Vries-Gleichung (mKdV-Gleichung) brachte,
![]() (5.3)
(5.3)
einer Gleichung, die ebenfalls viele Erhaltungssätze zuließ und, wie später gefunden wurde, auch eine Solitonengleichung ist. Die heute nach MIURA benannte Transformation
![]() (5.4)
(5.4)
vermittelt zwischen der KdV-Gleichung (5.2) und der mKdV-Gleichung (5.3). Diese Transformation ist eine Riccati-Gleichung für v, in der t nun nur noch ein Parameter ist. Mit der Substitution
![]()
(5.5)
und der Galileiinvarianz der KdV-Gleichung wird die Miuratransformation (5.4) zur zeitunabhängigen Schrödinger-Gleichung:
![]()
Das heißt, daß die zwischen KdV-Gleichung und mKdV-Gleichung vermittelnde
Transformation mit der Schrödinger-Gleichung zusammenhängt. Obwohl weder ψ,
noch λ, geschweige denn das Potential u,
die Lösung der KdV-Gleichung, bekannt waren, machte dieser Zusammenhang die
Sache sicherlich noch spannender, als sie sowieso schon war. CLIFFORD GARDNER
und JOHN GREEN waren mittlerweile zu KRUSKAL und MIURA hinzugestoßen und allen
vieren gelang die Lösung des Problems durch die Ausarbeitung der IST [GGKM
1967]. Schon kurz darauf, im Jahre 1968, formulierte LAX einen Beitrag zur
Verallgemeinerung der inversen Streumethode für andere Gleichungen der Form ut
= K(u, ux, uxx, ...) [Lax 1968]. Danach beruht die
Durchführung einer inversen Streumethode auf der Möglichkeit, zwei Operatoren
L = L(![]() ,
u, ux, ...) und A = A(
,
u, ux, ...) und A = A(![]() ,
u, ...) zu finden, die durch die Relation
Lt= [A,L] miteinander verknüpft sind. Die Operatoren L,
A werden heute Lax-Paar genannt.
,
u, ...) zu finden, die durch die Relation
Lt= [A,L] miteinander verknüpft sind. Die Operatoren L,
A werden heute Lax-Paar genannt.
Nach LAX dauerte es eine Weile, bis in der Theorie der Integration nichtlinearer partieller Differentialgleichungen weitere Fortschritte erzielt wurden.
"There was a great quietness after the 67 paper. And the integration of the KdV equation was thought to be a great exception."
So beschrieb DAVID KAUP die Jahre nach 1967 [persönliche Mitteilungen]. Es wurde vermutet, daß die Integration der KdV-Gleichung ein Einzelfall war, eine Singularität, ähnlich der Integration der Burgers-Gleichung durch die Cole-Hopf-Transformation. Doch diese Ansicht wurde 1971 durch ZAKHAROV und SHABAT [Zak., Sha. 1971] in Frage gestellt, denen es gelungen war, die IST auf die Nichtlineare Schrödingergleichung zu erweitern. Das ließ vermuten, daß es weitere integrable Evolutionsgleichungen geben könnte. Im Jahre 1972 fand in Potsdam, New York, eine Tagung über die mittlerweile bedeutend gewordenen besonderen nichtlinearen Wellen statt, auf der HARVEY SEGUR die Arbeit von ZAKHAROV und SHABAT vorstellte. KAUP erinnerte sich [persönliche Mitteilungen], daß vermutet wurde, auch die SG-Gleichung wäre mit der IST behandelbar. Die Frage war nur: wie? Das Ziel, eine allgemeine Lösungsmethode für bestimmte nichtlineare Differentialgleichungen zu erhalten, brachte MARK ABLOWITZ, DAVID KAUP, ALAN NEWELL und HARVEY SEGUR zu einer Zusammenarbeit. In einem gemeinsamen Seminar wurden Ansätze für Lösungsmöglichkeiten der SG-Gleichung und anderer Gleichungen vorgetragen. WADATIs Lösung der mKdV-Gleichung [Wadati 1972] wirkte beflügelnd auf die Arbeit. Als 1973 die SG-Gleichung als "4. Ausnahme" mit Hilfe der IST integriert werden konnte [AKNS 1973a], zeichnete sich eine Tendenz ab, die Anlaß zu der Vermutung gab, daß es eine ganze Klasse integrabler nichtlinearer Evolutionsgleichungen geben konnte. Noch im Jahre 1973 gelang es den Vieren, dies mit der heute nach ihnen benannten AKNS-Methode zu beweisen [AKNS 1973b, 1974]. Nach diesen Veröffentlichungen war die Reaktion zuerst eher verhalten, bevor die Arbeiten fünf bis zehn Jahre später ein "citation classic" wurden.
Die SG-Gleichung wurde zur gleichen Zeit unabhängig von LAMB [Lamb 1971], sowie von CAUDREY, GIBBON, EILBECK und BULLOUGH [CGEB 1973a, b] integriert und kurz darauf von FADDEEV und TAKHTADZHYAN [Newell 1985]. Viele neue und anspruchsvollere Probleme wurden nun angegangen. Und manche Entdeckungen stellten sich "nur" als Wiederentdeckungen schon älterer Arbeiten heraus, wie z.B. der von BURCHNALL und CHAUNDY [Bur., Cha. 1922, 1928, 1929].
Weiter zu Kapitel 5.3: Die Ausbreitung der Solitonentheorie