3.1 Die Entdeckung pseudosphärischer Flächen
Pseudosphärische Flächen sind durch eine konstante negative Gaußsche Krümmung K definiert, d.h.
![]()
Hierbei sind die Reziproken des kleinsten Krümmungsradius R1 und größten R2 in einem Punkt der Fläche die durch EULER so definierten Hauptkrümmungen k1 und k2. Bei Flächenpunkten negativer Gaußscher Krümmung weisen die Krümmungsradien in entgegengesetzte Richtungen; sie haben unterschiedliches Vorzeichen.
Lange vor der Entstehung der Theorie der Kurven und Flächen stand eine besondere pseudosphärische Fläche schon im Mittelpunkt mancher Untersuchungen: die Rotationsfläche der Traktrix um ihre Asymptote, die sogenannte Pseudosphäre. Deren Meridianlinie, die Traktrix (s. Abb. 3.1, Fig. 18), wurde schon 1676 von ISAAC NEWTON als die Kurve definiert, bei der die Länge der Tangente vom Tangentenpunkt bis zur x-Achse konstant ist [Stillwell 1990]. CHRISTIAN HUYGENS ebenso wie GOTTFRIED WILHELM LEIBNIZ interpretierten 1693 die Traktrix als Spur, die ein Stein zieht, der an einem Seil der Länge a gezogen wird von jemandem, der entlang der x-Achse läuft [Strubecker 1964]. (Daher der Name "Traktrix" von trahere = lat. ziehen.) HUYGENS untersuchte die Rotationsfläche der Traktrix und bestimmte deren Fläche, Inhalt und Schwerpunkt. Sie war ein Paradebeispiel für pseudosphärische Flächen und diente auch später immer wieder als Ausgangspunkt bei Untersuchungen zu Flächentransformationen. Ihren Namen bekamen die pseudosphärischen Flächen erst viel später durch EUGENIO BELTRAMI (1835 - 1900). In seiner Abhandlung zur nichteuklidischen Geometrie [Beltrami 1866] stellte er mit diesem Namen ("pseudosferiche") die pseudosphärischen Flächen der Kugel (Sphäre) mit positiver Krümmung K gegenüber. BELTRAMI stellte den Zusammenhang zwischen der Differentialgeometrie einerseits und der nichteuklidischen Geometrie LOBA_EVSKIJs und BOLYAIs andererseits her [Dieudonné 1990]. Er war 1866 Hinweisen von GAUSS gefolgt, der in Briefen an SCHUMACHER angeregt hatte, die Verbindung zwischen der Differentialgeometrie der Flächen konstanter Krümmung und der nichteuklidischen Geometrie der Ebene zu suchen [Scholz 1980]. Danach ist in der Pseudophäre eine lokale euklidische Realisierung der nichteuklidischen Ebene zu sehen.
Das Problem der Abwickelbarkeit von Flächen zieht sich wie ein roter Faden durch die differentialgeometrische Entwicklungslinie der Solitonentheorie.
(Bis zu GAUSS "Disquisitiones" von 1828 wurden als "abwickelbar" alle diejenigen Flächen bezeichnet, die ohne Verzerrung in die Ebene ausgebreitet werden können. Erst GAUSS erweiterte den Begriff "abwickelbar" auch auf Paare im Raum gekrümmter Flächen und kam damit zu dem, was heute mit Isometrie beschrieben wird; wobei zu jener Zeit noch nicht zwischen lokal und global unterschieden wurde [Dieudonné 1990].)
Es führte die Mathematiker EDMOND BOUR (1832 - 1866) [Kurzbiographie], OSSIAN PIERRE BONNET (1819 - 1892) [Kurzbiographie] und ALFRED ENNEPER (1830 - 1885) [Kurzbiographie] auf verschiedenen Wegen zur SG-Gleichung und lieferte die Motivation zur Entwicklung der Bianchitransformation, aus der später die Bäcklundtransformation entstand. Die erste systematische Untersuchung zur Abwickelbarkeit von Flächen stellte CARL FRIEDRICH GAUSS (1777 - 1855) an, der sich seit 1816 mit den Problemen der Abwickelbarkeit von Flächen beschäftigt hatte und wohl den größten Beitrag zur Entwicklung der klassischen Differentialgeometrie überhaupt leistete. In seinen systematischen Studien von Flächen ging er von der Eulerschen Parameterdarstellung von Flächen aus:
![]()
Zur Klärung von EULERs Frage, welche Bedingungen diese Funktionen erfüllen müssen, damit die dazugehörige Fläche auf eine Ebene abwickelbar ist, entwickelte GAUSS den Begriff der Bogenlänge s der Fläche. Der Ausdruck
![]()
wird, ausgedrückt in den Parametern u und v, zur ersten Fundamentalform der Fläche:
![]()
(Moderne Schreibweise der Gaußschen Symbole: E = g11 , F = g12 , G = g22 .)
GAUSS führte die innere Geometrie der Fläche ein und stellte fest, daß alle inneren Eigenschaften und insbesondere die später nach ihm benannte Gaußsche Krümmung K der Fläche schon durch die Größen E, F, und G bestimmt sind. GAUSS zeigte ferner die Umkehrung, daß die inneren Eigenschaften einer Fläche durch die Krümmung der Fläche bestimmt sind, sowie daß solche Eigenschaften unter Biegung ohne Verzerrungen der Fläche erhalten bleiben und insbesondere die Krümmung K biegungsinvariant ist [Gauß 1828]. Als "theorema egregium" (exzellentestes Theorem) bezeichnete er sein Ergebnis, daß abwickelbare Flächen die gleiche Gaußsche Krümmung in korrespondierenden Punkten haben.
FERDINAND MINDING (1806 - 1885) [Kurzbiographie], der Schüler von GAUSS war, setzte dessen Arbeiten zur Flächentheorie fort. Er untersuchte 1830 Flächen konstanter Gaußscher Krümmung und berechnete u.a. deren Linienelement in geodätischen Polarkoordinaten [Minding 1830a, b]. Im Jahre 1838 stellte er allgemeinere Untersuchungen zu Flächen an, die auf Rotationsflächen abwickelbar sind [Minding 1838]. Kurz darauf bewies er eine Umkehrung von GAUSS theorema egregium, nämlich daß Flächen, die in korrespondierenden Punkten gleiche Gaußsche Krümmung haben, lokal aufeinander abwickelbar sind [Minding 1839]. Es lag für eine Beispielbetrachtung nahe, die Krümmung K konstant zu wählen. MINDING untersuchte auf diese Weise Flächen konstanter Gaußscher Krümmung, unter ihnen auch einige pseudosphärische Flächen. Zur Bestimmung dieser Flächen integrierte MINDING die später so genannte Monge-Ampèresche Gleichung für Flächen konstanter Gaußscher Krümmung K
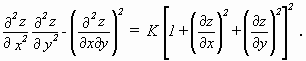 (3.1)
(3.1)
Er grenzte seine Untersuchungen ein, indem er nur Rotationsflächen konstanter Krümmung betrachtete. Für diesen Fall konnte er Gleichung (3.1) in Polarkoordinaten umschreiben:
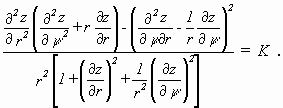 (3.2)
(3.2)
Die weitere Einschränkung, nur Rotationsflächen konstanter Spindel-Ganghöhe zu betrachten, also
![]()
ließ ihn zu folgendem Integral kommen:
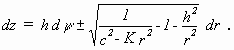 (3.3)
(3.3)
MINDING unterschied Umdrehungsflächen mit h = 0 von Schraubenflächen mit h ¹ 0. Je nach Wert der Konstanten c in Integral (3.3) unterteilte er die Umdrehungsflächen konstanter negativer Krümmung nun in drei Typen. Deren Meridianlinie gab er an, also diejenige Kurve, für die dψ = 0, d.h. durch deren Umdrehung längs der z-Achse die Rotationsfläche entsteht:
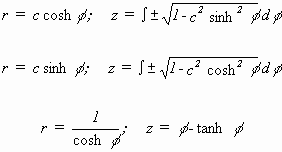 (3.4a)
(3.4a)
(3.4b)
(3.4c)
Diese drei Typen wurden später pseudosphärische Flächen des hyperbolischen, elliptischen und parabolischen Typs genannt [Lilienthal 1903] [Eisenhart 1909]. Im parabolischen Fall ist die Meridiankurve die Traktrix und die Fläche ist die Pseudosphäre (s. Abb. 3.1, Fig. 18).
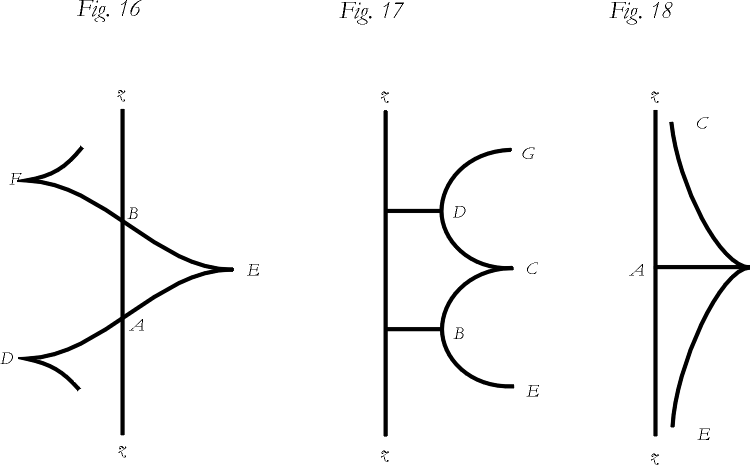
Abbildung 3.1:
Mindings pseudosphärische Flächen. Abbildung aus [Minding 1839]. Fig. 16: Meridiankurve der pseudosphärischen Fläche des elliptischen Typs (Gleichung 3.4b); Fig. 17: Der hyperbolische Typ (Gleichung 3.4a); Fig. 18: Der parabolische Typ (Gleichung 3.4c).
Nach MINDINGs Arbeiten zu abwickelbaren Flächen verging eine geraume Weile, bis weitere pseudosphärische Flächen untersucht wurden. Im Jahre 1865 stellte ULISSE DINI (1845 - 1918) fest [Dini 1865], daß die Traktrix die Profilkurve einer Schar von pseudosphärischen Schraubenflächen ist [Voss 1903]. Sie entstehen kinematisch gesehen, indem die Traktrix (Abb. 3.1, Fig. 18) um ihre Asymptote gedreht wird und sich dabei längs der Asymptote verschiebt. Die Ganghöhe h ist dabei ein frei wählbarer Parameter.
Eine andere Entwicklung, die zur Entdeckung weiterer pseudosphärischer Flächen führte, verlief über die Joachimsthalschen Flächen. FERDINAND JOACHIMSTHAL (1818 - 1861) behandelte 1846 Flächen, deren eine Schar von Hauptkrümmungslinien auf Ebenen liegen, die alle eine gemeinsame Gerade enthalten [Joachimsthal 1846]. Sie tragen heute seinen Namen. ALFRED ENNEPER untersuchte 1868 Joachimsthalsche Flächen konstanter Krümmung [Enneper 1868], die heute Enneperflächen genannt werden. Ennepersche Flächen positiver bzw. negativer Gaußscher Krümmung wurden in den Dissertationen von Ennepers Doktoranden G. BOCKWOLDT und E. LENZ eingehend untersucht [Fischer 1986], [Mel., Ste. 1994]. Zeichnungen verschiedener Enneperflächen stellte [Mel., Ste. 1994] vor. Eine relativ einfache pseudosphärische Fläche, die LENZ übersehen hatte, wurde 1884 von THEODOR KUEN entdeckt [Kuen 1884]. Eine detaillierte Beschreibung der Kuenschen, sowie der Dinischen Fläche und der Pseudosphäre mit Fotos und weiteren Zeichnungen ist in [Fischer 1986] zu finden.
Das Interesse an der Geometrie von besonderen Flächen, und damit an der Gestalt der pseudosphärischen Flächen, erlosch im wesentlichen innerhalb der Differentialgeometrie um die Jahrhundertwende. In der Mathematik rückten allgemeinere und abstraktere Gesichtspunkte in den Vordergrund [Fischer 1986]. Bildhaft für diese Entwicklung stellt sich der Bau von Modellen besonders interessanter Flächen dar, der im letzten Drittel des vergangenen Jahrhunderts seinen Höhepunkt erlebte und nach dem 1. Weltkrieg ganz zum erliegen kam. Was die pseudosphärischen Flächen betrifft, so mag HILBERTS Beweis, daß Flächen mit K = -1 nie vollständig im R3 sind, sie also dort immer Singularitäten zeigen [Hilbert 1901], mit ein Grund für das nachlassende Interesse an ihnen sein. In der durch FRIEDMANN und LEMAITRE begründeten Standardkosmologie ist der physikalische Raum von konstanter Krümmung. Diese Kosmologie setzte sich aber erst in den 30er und 40er Jahren durch und motivierte in der Folge die erneute Beschäftigung mit der nichteuklidischen Geometrie.
Weiter mit Kapitel 3.2: Die Sinus-Gordon-Gleichung als Gleichung für pseudosphärische Flächen