[Inhaltsverzeichnis]

Mit MINDINGs Betrachtungen 1839 waren pseudosphärische Flächen zum ersten Mal ausführlich diskutiert worden. Die Formen, die er für die pseudosphärischen Flächen angab, entsprechen jedoch keinen Solitonenlösungen, da Gleichung (3.2) keine Solitonengleichung ist. Die Wahl der Parameterlinien, die zur Beschreibung der Fläche gewählt werden, entscheidet über das Aussehen der Gleichung für die Fläche. MINDINGs Wahl der Geodätischen als Parameterlinien ψ = const. und geodätisch parallelen Kurven als Parameterlinien φ = const. führen zu keiner Solitonengleichung. Zu einer Solitonengleichung, nämlich der SG-Gleichung, führt erst die Wahl der Hauptkrümmungslinien oder der Asymptotenlinien als Parameterlinien der pseudosphärischen Fläche. Die Hauptkrümmungslinien einer Fläche verlaufen in jedem Punkt per definitionem in den Richtungen größter bzw. kleinster Krümmung. Sie stehen stets senkrecht aufeinander. In den Asymptotenrichtungen verschwindet, per definitionem, die 2. Fundamentalform. Die Asymptotenlinien folgen den Asymptotenrichtungen. Sie bilden auf einer Fläche konstanter Gaußscher Krümmung ein sogenanntes "Tschebyschevsches Netz". Die erste Fundamentalform wird ihnen angepaßt zu

d.h. E = G = 1, F = -cos Φ, Φ = Winkel zwischen den Asymptotenlinien. Eingesetzt in die Gaußsche Gleichung für die Krümmung:

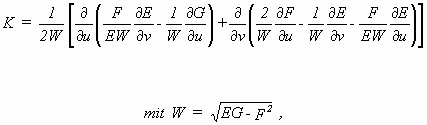
ergibt sich damit die SG-Gleichung mit den beiden Scharen der Asymptotenlinien u = const. und v = const. als Parameterlinien:

(3.5a)

Der italienische Mathematiker LUIGI BIANCHI (1856 - 1929) nannte die SG-Gleichung Fundamentalgleichung für Flächen konstanter negativer Krümmung [Bianchi 1910]. Bei der Wahl der Hauptkrümmungslinien als Parameterlinien mit φ = halber Winkel zwischen den Asymptotenlinien, also 2φ = Φ, wird die erste Fundamentalform zu

und die aus der Gaußschen Gleichung resultierende Form der SG-Gleichung ist

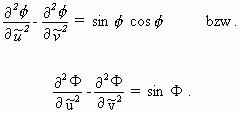
(3.5b)

Die Parameter zu den Hauptkrümmungslinien (getildete Variablen) und zu den Asymptotenlinien (ungetildete Variablen) sind leicht ineinander transformierbar:

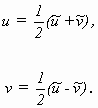
(3.6)

Verschiedene Solitonenlösungen der SG-Gleichung beschreiben, bei geeigneter Darstellung, verschiedene pseudosphärische Flächen. In der einfachsten von ihnen, der Pseudosphäre, findet man die Ein-Solitonenlösung der SG-Gleichung für u(tilde) = const. wieder:

(3.7)

Lösung (3.7) zeigt den Verlauf der sogenannten stationären Versetzungslösung oder kink solution der SG-Gleichung (s. Kapitel 4, Abb. 4.5). Wird die Bedingung u(tilde) = const. fallengelassen, so beschreibt die Lösung

die Dinifläche, also die Schraubenfläche der Pseudosphäre, mit der Ganghöhe h. Die Kuensche Fläche ist ein Abbild der Zwei-Solitonenlösung der SG-Gleichung.

Die Wahl der Parameterlinien entscheidet, wie gesagt, über das Aussehen der charakteristischen Gleichung einer Fläche und auch darüber, ob die Gleichung eine Solitonengleichung ist oder nicht. Bei der Wahl völlig anderer, nicht so leicht in die Asymptotenlinien transformierbarer Koordinatenlinien können sich andere Solitonengleichungen ergeben. Nach [Popov 1993] führt der Ansatz

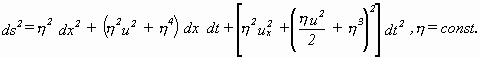
zur modifizierten KdV-Gleichung als charakteristische Gleichung für pseudosphärische Flächen:

Der alternative Ansatz

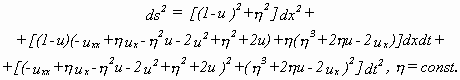
führt laut derselben Quelle zur KdV-Gleichung:

Durch besondere Wahl des Linienelements ds können auch nichtsolitonische partielle Differentialgleichungen als charakteristische Gleichung für pseudosphärische Flächen erzeugt werden, z.B. die Burgers-Gleichung oder die Liouvillegleichung. Das Auftauchen anderer Solitonengleichungen als der SG-Gleichung in der klassischen Differentialgeometrie der Kurven und Flächen im Kontext mit pseudosphärischen Flächen ist mir allerdings nicht bekannt.

Die Hauptkrümmungslinien oder die Asymptotenlinien (sie werden in der Literatur jener Zeit als Haupttangentenkurven, später auch als Schmiegetangentenkurven bezeichnet) zählen zu den Kurvenscharen, die meist erst nach den geodätischen Linien untersucht wurden. Wie die Hauptkrümmungslinien sind die Asymptotenlinien Objekte der "äußeren" oder "extrinsischen" Geometrie. Das heißt, daß sie empfindlich auf (längentreue) Verbiegung der Fläche reagieren. Es ist daher nicht verwunderlich, daß im Zusammenhang mit der Abwickelbarkeit (Verbiegung) von Flächen andere Parameterlinien bevorzugt wurden. Und Flächen konstanter Krümmung fanden eben besonders bei Untersuchungen zur Abwickelbarkeit von Flächen Verwendung. Eine Vielzahl von Gleichungen wurde so im Zusammenhang mit Flächen konstanter Krümmung in der klassischen Differentialgeometrie behandelt. Eine Übersicht über die Geometrie von Solitonengleichungen geben [Mel., Ste. 1994] und [Bobenko 1994]. Hierbei wurden auch andere als pseudosphärische Flächen untersucht, die Solitonenlösungen wiedergeben, wie z.B. Flächen, die BIANCHI untersuchte [Bianchi 1910] und die heute als "Multibubbletons" bekannt sind [Mel., Ste. 1994].

Dabei wurden auch Solitonengleichungen gefunden, freilich ohne diese als solche zu erkennen. So betrachtete z.B. JULIUS WEINGARTEN (1836 -1910) 1863 die auf eine Kugel abwickelbaren Flächen, also Flächen mit konstanter positiver Krümmung [Weingarten 1863] und setzte die erste Fundamentalform so an:

(WEINGARTENs Untersuchungen in dieser bekannten Arbeit führen zu den Weingartenschen Flächen oder W-Flächen, die dadurch gekennzeichnet sind, daß ein Hauptkrümmungsradius eine Funktion des anderen ist: R₁ = f (R₂).)

Auf obigem Wege über die Gaußsche Gleichung für die Krümmung gelangte er zu der integrablen hyperbolischen Sinh-Gordon-Gleichung

(3.8)

die nach [Beutler 1993] Solitonenlösungen besitzt. Gleichung (3.8) trug allerdings im Verlauf der frühen Periode der Solitonentheorie nicht zu der Entwicklung der Solitonentheorie bei. Daher sollen hier nur die Arbeiten weiter verfolgt werden, die sich mit pseudosphärischen Flächen, der SG-Gleichung und deren Transformationen beschäftigten.

Ein offenes Problem war, wie alle auf eine gegebene Fläche abwickelbaren Flächen gefunden werden konnten. Dieses Problem wird heute nach BOUR benannt, da EDMOND BOUR (1832 - 1866) in dieser Frage mit seiner Arbeit "Théorie de la déformation des surfaces" [Bour 1862a] einen ersten Fortschritt erzielte. Was diese Arbeit für die Geschichte der Solitonentheorie bedeutend macht ist, daß ihr der Ruhm der Priorität an der SG-Gleichung zukommt: Die SG-Gleichung erschien erstmalig explizit in dieser Arbeit von BOUR im Jahre 1862. Wobei zu bemerken ist, daß die SG-Gleichung von BOUR nicht im Zusammenhang mit pseudosphärischen Flächen gesehen wurde. Im Jahre 1860 stellte die Pariser Akademie die Preisaufgabe, Flächen zu finden und in einer einfachen Weise anzugeben, die auf eine gegebene Fläche abwickelbar sind. Den ersten Preis gewann BOUR mit der oben erwähnten Arbeit sowie ihrer Fortsetzung [Bour 1862b]. Es sind dies BOURs einzigen großen Arbeiten zur Differentialgeometrie. Ein dritter Teil war zwar geplant, doch Bour starb schon 1866 im Alter von nur 33 Jahren. Diese beiden Arbeiten BOURs wurden von Zeitgenossen außerordentlich geschätzt [Reich 1973]. Sie zeigen, daß jede auf eine gegebene Fläche abwickelbare Fläche (lokal) einer Monge-Ampèreschen Gleichung genügt [Dieudonné 1990]. Und sie enthalten die später sogenannten Mainardi-Codazzi-Gleichungen für den speziellen Fall, daß die Parameterlinien die geodätischen Linien sind.

Im seiner "Théorie de la déformation des surfaces" [Bour 1862a], dem ersten Teil der Preisarbeit, entwickelte BOUR verschiedene Wege, alle auf eine gegebene Fläche abwickelbaren Flächen zu finden. Der erste und rein analytische Weg führt durch den Gebrauch symmetrischer Koordinaten zu einer Differentialgleichung, deren Integration BOUR in einer früheren Arbeit geleistet hatte [Bour 1857]. Auf dem zweiten Weg erhielt BOUR mit Hilfe geodätischer Linien und zugehörigen "Perpendikularen" als Parameterlinien eine Reihe sekundärer Gleichungen, die BOUR "Fundamentalgleichungen" nannte, und aus denen sich, nach BOURs Meinung, die ganze Theorie der Flächen ergab. BOUR wandte diese Gleichungen direkt auf das gestellte Problem an und bestimmte so die auf Rotationsellipsoide, Hyperboloide und Schraubenflächen abwickelbaren Regelflächen. Weiterhin folgerte BOUR, daß alle Schraubenflächen auf jeweils eine Rotationsfläche abwickelbar sind.

Eine der dabei auftretenden Fundamentalgleichungen beinhaltet die SG-Gleichung. Diese Fundamentalgleichung führte BOUR wie folgt ein [Bour 1862a, S. 120]:

"Auparavant, pour terminer ce chapitre, j´indiquerai rapidement une forme nouvelle et curieuse, que l´on peut donner à l´équation différentielle des surfaces applicables sur les surfaces de révolution. J´ai cru devoir donner cette équation à cause de sa simplicité, et de la facilité avec laquelle elle s´établit au moyen des équations fondamentales; je l´ai reléguée ici, parce que cette forme n´ést point celle qui m´a servi dans les applications, soit géométriques, soit analytiques."

 

(Zuvor, um das Kapitel abzuschließen, gebe ich schnell eine neue und erstaunliche Form an, die man zu den Differentialgleichungen der auf die Rotationsflächen abwickelbaren Flächen hinzurechnen kann. Ich habe geglaubt, diese Gleichung wegen ihrer Einfachheit angeben zu müssen, und weil sie sich leicht in die Fundamentalgleichungen einfügt. Ich habe sie hierher verbannt, weil diese Form mir nicht bei den Anwendungen geholfen hat, weder bei den geometrischen noch bei den analytischen.)

Die Fundamentalgleichung nimmt die einfache Gestalt an

(3.9)

und ist ein Ausdruck für die geodätische Krümmung Z₁ (heutige Bezeichnung k_g) der zu den geodätischen u-Linien (v = const.) senkrechten v-Linien (u = const.) einer auf eine Rotationsfläche abwickelbaren Fläche. Die Gleichungen für die abhängigen Variablen ζ₁ und ζ in Abhängigkeit von dem Parameter u lauten bei BOUR

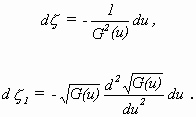(3.10a)

(3.10b)

Was die unabhängige Variable η in Gleichung (3.9) angeht, so zeigte BOUR nur, daß sie existiert, ohne weiter auf ihre Eigenschaften (Charakterisierung der Kurven η = const.) einzugehen. BOURs bevorzugtes Anwendungsbeispiel für seine Gleichungen ist in seiner ganzen Arbeit das Katenoid, also die Rotationsfläche der Kettenlinie. Für das Katenoid lautet die 1. Fundamental-form mit u,v = geodätische Polarkoordinaten:

(3.11)

also E = 1, F = 0 und G(u) = (1+u²). Die geodätische Krümmung der v-Linien ist bei orthogonalen Flächenparametern u,v gegeben durch

Und für die geodätische Krümmung der v-Linien des Katenoids folgt mit Gleichung (3.11)

(3.12)

Aus der von BOUR durchgeführten Umparametrisierung (Gleichung 3.10a) folgt

mit c = Integrationskonstante (o.B.d.A. = 0). Daraus ergibt sich für die geodätische Krümmung der v-Linien des Katenoids (Gleichung 3.12)

Da ferner aus den Gleichungen (3.10a,b) für das Katenoid mit G = (1+u²) folgt ζ₁ = ζ, erhielt BOUR aus seiner Fundamentalgleichung (3.9) in der Anwendung auf das Katenoid die SG-Gleichung

(3.13)

Sie ergibt sich aus der geodätischen Krümmung für den Fall, daß die Fundamentalform (3.11) Gültigkeit besitzt und unter Anwendung der abhängigen Variablen ζ aus Gleichung (3.10a) und den speziellen Parametern η und v.

Es stellt sich die Frage, wozu BOUR die speziellen Parameter η und v und die Variable ζ einführte. Die Antwort lieferte BOUR selber in dem oben zitierten Absatz: Auf diesem Wege ergibt sich eine einfache Gleichung (Gleichung 3.9) für die geodätische Krümmung. Weitere Anwendungen fand BOUR für diese Fundamentalgleichung, deren Spezialfall die SG-Gleichung ist, nicht. Um so erstaunlicher ist es, daß BOUR ohne großes Federlesen ("... on trouve aisément l´integrale particulière ...") eine exakte Lösung der SG-Gleichung angab und zwar für die SG-Gleichung in beiden heute gebräuchlichen Formen. Die Lösung der Form (3.13) gab er an mit

wobei k das Modul der elliptische Funktion sinus amplitudinis ist; m, n, l und k sind Konstanten von denen drei frei gewählt werden können. Des weiteren lieferte BOUR die durch die einfache Parametertransformation (3.8) erhältliche Form der SG-Gleichung

mitsamt einer exakten Lösung

Mit diesen Lösungen schloß BOUR das lange Kapitel seiner Arbeit, in dem er sich mittels der Fundamentalgleichungen um die Darstellung der auf eine gegebene Fläche abwickelbaren Flächen bemühte. Die Gleichung (3.9) oder die SG-Gleichung finden im weiteren Verlauf seiner Arbeit keine Erwähnung mehr.

Den zweiten Preis der Pariser Akademie für das Auffinden der auf eine gegebene Fläche abwickelbaren Flächen erhielt DELFINO CODAZZI (1824 - 1873), der die Mainardi-Codazzi-Gleichungen in etwas allgemeinerer Form darstellte. Und den dritten Preis erhielt OSSIAN PIERRE BONNET (1819 - 1892) mit der Arbeit "Mémoire sur la théorie des surfaces applicables sur une surface donnée" [Bonnet 1865], die vor allem den heute sogenannten Gauß-Bonnetschen Satz enthält. In der Fortsetzung seiner Preisarbeit [Bonnet 1867] bewies BONNET das heute als Fundamentalsatz der Flächentheorie (oder Bonnet-Theorem) bezeichnete Theorem, wonach die sechs vorgegebenen Funktionen der ersten und zweiten Fundamentalform eine Fläche bis auf ihre Lage im Raum vollständig beschreiben. 

(Ein den heutigen Exaktheitsvorstellungen gerecht werdender Beweis dieses Satzes gelang zuerst KARL PETERSON (1828 - 1881) in seiner Kandidatenschrift (Doktorarbeit) aus Dorpat in Estland (heute Tartu) im Jahre 1853 [Reich 1973].)

BONNETs Arbeit von 1867 enthält ebenfalls die SG-Gleichung und zwar zum ersten Mal in dem heute bekannten Zusammenhang mit pseudosphärischen Flächen. BONNET untersuchte die Eigenschaften zweier Flächen, deren Hauptkrümmungslinien durch eine einfache Transformation ineinander übergehen. Die Bestimmung dieser Flächen hing von der Integration u.a. der SG-Gleichung ab, wie BONNET bemerkte, die jedoch "jenseits der Möglichkeiten der derzeitigen Analyse" lag. Er bemerkte [Bonnet 1867, S. 70]:

"Cette integration est au-dessus des forces de l´Analyse actuelle, mais on peut, sans l´effectuer, parvenir à une définition géométrique simple des surfaces dont il s´agit."

(Diese Integration liegt jenseits der Möglichkeiten der derzeitigen Analyse, aber man kann auch ohne das zu bewerkstelligen zu einer einfachen geometrischen Definition jener Flächen, um die es sich handelt, kommen.)

BONNET zeigte im folgenden dann mit einigen Rechnungen, daß die Flächen, auf denen die transformierten Krümmungslinien liegen auf eine "imaginäre Kugel" (sphère imaginaire) abwickelbar sind, womit er die Flächen konstanter negativer Gaußscher Krümmung meinte. Interessanterweise taucht hier der Name "sphère imaginaire" auf, ein Jahr nachdem BELTRAMI den Namen "pseudosferiche" prägte [Beltrami 1866]. BELTRAMIs Begriff "pseudosphärische Flächen" setzte sich gegen den aus BONNETs Namen ableitbaren Begriff "imaginärsphärische Flächen" durch.

Eine dritte Erwähnung der SG-Gleichung kurz nach BOUR und BONNET sollte nicht unberücksichtigt bleiben. Der Göttinger Mathematikprofessor ALFRED ENNEPER (1830 - 1885) bearbeitete in den sechziger Jahren des letzten Jahrhunderts intensiv die Flächentheorie. Im fünften Teil einer Reihe von Abhandlungen ("Analytisch-geometrische Untersuchungen") [Enneper 1868] betrachtete er ausführlich Flächen konstanter Krümmung und leitete für diese "fundamentale Gleichungen" ab, wie er sie nannte, darunter auch die SG-Gleichung. Ob ihm die Arbeit BOURs oder sogar schon BONNETs Arbeit bekannt war, ist ungewiß; Erwähnung finden sie bei ENNEPER nicht. Diese und eine weitere Arbeit ENNEPERs [Enneper 1870] galten bis vor kurzem als die ersten, in denen die SG-Gleichung Erwähnung fand. Das belegen Äußerungen in z.T. vielzitierten Arbeiten [Mel., Ste. 1993], [Seeger 1980a, 1983, 1985, 1993], [Ogurtani 1983], [MNS 1991], [Seg., Wes. 1981], [Beutler 1993]. Daher war in den fünfziger Jahren dieses Jahrhunderts von ALFRED SEEGER vorgeschlagen worden, die SG-Gleichung "Ennepergleichung" zu nennen, ein Name, der in der deutschsprachigen Literatur zur Solitonentheorie noch bis heute zu finden ist [Seeger 1983, 1985], [See., Wes. 1981], [MNS 1991], [Beutler 1993]. Hinweise auf die Arbeit von BONNET von 1867 im Zusammenhang mit der SG-Gleichung lieferte NEIL IBRAGIMOV in seinem Buch [Ibragimov 1983], S. 222, der die Bezeichnung "Bonnet-Gleichung" für die SG-Gleichung verwendete. IBRAGIMOV berief sich auf eine Arbeit SOPHUS LIEs [Lie 1881], der auf die SG-Gleichung in BONNETs Arbeit hinwies, und zitierte BONNET nicht direkt. Die Arbeit von BOUR wurde allerdings bisher übersehen. In einer Kurzmitteilung habe ich darauf hingewiesen [Heyerhoff 1995].

Kurz soll auch auf die SG-Gleichung in ENNEPERS Arbeiten eingegangen werden. ENNEPERs Ziel war es, für Flächen konstanter Krümmung allgemeine Gleichungen abzuleiten [Enneper 1868, S. 258]. Und er bemerkte:

"Die unüberwindlichen Schwierigkeiten, welche sich bei der Aufsuchung aller Flächen von constantem Krümmungsmaass entgegenstellen, führen von selbst darauf, besondere Fälle zu betrachten und die Fläche noch durch eine zweite geometrische Eigenschaft näher zu bestimmen, wobei dann die Wahl der Curvensysteme nicht gleichgültig ist."

ENNEPER stellte sich daher die Frage:

"Für welche Flächen von constantem Krümmungsmaass ist ein System von Krümmungslinien plan oder sphärisch?"

Diese Frage führt zu Joachimsthalschen Flächen konstanter Krümmung, die heute Ennepersche Flächen genannt werden (s.o.). Für Flächen dieser Art mit negativer konstanter Krümmung kam ENNEPER direkt auf die SG-Gleichung, allerdings in dieser etwas ungewohnten Form:

Diese Gleichung entspricht der SG-Gleichung, lediglich wurde anstatt des Φ in Gleichung (3.5b), womit wieder der Winkel zwischen den Asymptotenlinien bezeichnet ist, von ENNEPER "arctan t" gewählt. Es sei angemerkt, daß bei der Substitution

Ennepers Gleichung zur SG-Gleichung wird.

Die Hauptkrümmungslinien der pseudosphärischen Flächen erfüllten ENNEPERs Bedingungen und brachten ihn seinem Ziel näher, grundlegende Gleichungen für Flächen negativer konstanter Krümmung zu finden. Allerdings schien ENNEPER mit der SG-Gleichung nicht zufrieden zu sein, weil ihm ihre allgemeine Integration nicht möglich war, wie er bemerkte. Daher ging er im weiteren Verlauf nicht mehr in nennenswerter Weise auf sie ein. Zwei Jahre später erwähnt ENNEPER sie in der Form (3.5a) noch einmal [Enneper 1870] und stellte fest, daß jedem Integral der Gleichung nur eine Fläche entspricht.

Die bekannteste Erwähnung der SG-Gleichung in der klassischen Differentialgeometrie stammt von P. L. TSCHEBYSCHEV aus dem Jahre 1878 [Tschebyschev 1878]. Ihr, oder sogar noch späteren Arbeiten anderer Mathematiker, wird bis heute noch verschiedentlich die Priorität an der SG-Gleichung zugesprochen [Popov 1993], [McLachlan 1994]. TSCHEBYSCHEV führte in seinem Beitrag das heute nach ihm benannte Tschebyschevsche Netz ein. In ihm sind in einem Viereck, das aus Kurven der beiden Scharen der Parameterlinien auf einer Fläche gebildet wird, die jeweils gegenüberliegenden Seiten gleich lang. Der originelle Beitrag des bekannten russischen Mathematikers bestand darin, anzugeben, wie ein gewebter Stoff, der eine eng anliegende Hülle für einen Gegenstand beliebiger Form bilden soll, zuzuschneiden ist. Dabei bediente sich TSCHEBYSCHEV folgenden Tricks: In jedem Punkt des an dem Gegenstand anliegenden Stoffes kreuzen sich zwei, als unelastisch angenommene, Fäden in einem Winkel Φ zwischen 0° und 180° . Fährt man mit dem Finger entlang eines Fadens, so variiert dieser Winkel unter Umständen. Der Stoff ist nun dort zu schneiden, wo Φ das Intervall [0° , 180° ] verläßt. TSCHEBYSCHEV zeigte, daß Φ der Gleichung

gehorcht, wobei K die Gaußsche Krümmung des entsprechenden Punktes der Oberfläche des zu umhüllenden Gegenstandes ist. Im Falle der pseudosphärischen Flächen bilden die asymptotischen Linien gerade ein TSCHEBYSCHEVsches "Stoffnetz".

Weiter zu Kapitel 3.3: Die Bianchi- und die Lietransformation

[Inhaltsverzeichnis]