3.5 Zur weiteren Entwicklung der Theorie der
Bäcklundschen Transformationen
Die bis hierher geschilderten Entwicklungen in der frühen Periode der Solitonentheorie wurden bei Beginn der klassischen Phase wieder aufgenommen. Sie trugen zu deren Etablierung mit bei. Weitere Entwicklungen zur Bäcklundtransformation, die zeitlich gesehen auch innerhalb der frühen Periode der Solitonentheorie gemacht wurden, wurden in der klassischen Periode erst später mit der Solitonentheorie in Verbindung gebracht. Sie gehören daher nicht eigentlich zur frühen Geschichte der Solitonentheorie. Diese neueren Entdeckungen sind recht vielfältig und die Forschungen sind bis heute nicht abgerissen. Des Überblicks halber seien hier einige - weniger bekannte - hier kurz gestreift.
Die Theorie der Bäcklundschen Transformationen ist um die Jahrhundertwende häufig bearbeitet worden. Dabei war die Verallgemeinerung der Bäcklundtransformation vorrangiges Ziel [Lamb 1976]. Es wurden Versuche unternommen, Bäcklundsche Transformationen für weitere Differentialgleichungen zu finden und sie somit für weitere Probleme innerhalb der Theorie der Differentialgleichungen nutzbar zu machen. Ein Beispiel dafür sind die Arbeiten von JEAN CLAIRIN [Clairin 1900 - 1913], der nach einer Methode suchte, welche Bäcklundtransformationen für beliebige Gleichungen produzierte, falls sie existieren. Eine kurze Beschreibung einiger Arbeiten CLAIRINs, seiner Methode nebst Beispielen findet sich in [Lamb 1976]. Eine weitere Förderung erfuhr die Theorie der Bäcklundtransformation durch EDOUARD GOURSAT [Goursat 1902a, b - 1925], die z.T. in [Liebmann 1914] beschrieben werden.
In der Lehrbuchliteratur wurde die Bäcklundtransformation sowohl von DARBOUX [Darboux 1887] als auch von BIANCH [Bianchi 1894, 1910] sehr ausführlich bearbeitet. Mit dem Lehrbuch von EISENHART [Eisenhart 1909] wurde die Bäcklundtransformation erstmalig in englischer Sprache vorgestellt. Somit lagen umfangreiche und bekannte Lehrbücher in italienischer, deutscher, französischer und englischer Sprache vor, die die Bäcklundtransformation eingehend darstellten. Trotzdem geriet sie - wie weite Teile der Differentialgeometrie überhaupt - für lange Zeit in Vergessenheit.
1992 machte SERGUEI TSAREV [Tsarev 1992] darauf aufmerksam, daß die Bullough-Dodd-Gleichung
![]()
ebenfalls eine Solitonengleichung, schon 1910 von dem rumänischen Mathematiker G. TZITZÉICA behandelt wurde [Tzitzéica 1910], und zwar in der Form:
![]()
TZITZÉICA gab auch das dazugehörige lineare Differentialgleichungsproblem sowie die Bäcklundtransformation dazu an.
Auf eine weitere Verknüpfung der Solitonentheorie mit der klassischen Differentialgeometrie machte B. A. DUBROVIN aufmerksam [Dubrovin 1990]. Von ihm kommt der Hinweis, daß das durch die IST integrable Drei-Wellen-System mit dem Egorov-Koordinatensystem zusammenhängt. TSAREV bemerkt hierzu [Tsarev 1992], daß solch ein System schon 1866 von DARBOUX angeregt worden ist, der 1910 dieses System Egorov-System nannte [Darboux 1910]. D. TH. EGOROV griff 1901 in seiner Doktorarbeit DARBOUXs Gedanken von 1866 auf [Egorov 1901] und BIANCHI fand 1915 die dazugehörige Bäcklundtransformation und die Superpositionsgleichung [Bianchi 1915].
Eine große Fülle von Lösungen der SG-Gleichung der Form
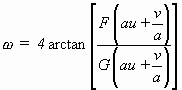
wurde von RUDOLPH STEUERWALD angegeben [Steuerwald 1936]. Er behandelte die Enneperschen Flächen, insbesondere die mit negativer Gaußscher Krümmung, sehr ausführlich und lieferte eine gründliche Diskussion ihrer Bäcklundtransformationen.
Infinitesimale Bäcklundtransformationen wurden von CHARLES LOEWNER behandelt [Loewner 1952].
Im Zusammenhang mit Solitonen wurde nur die Bäcklundtransformation für die SG-Gleichung sehr früh, nämlich 1953, von ALFRED SEEGER, HANS DONTH und ALBERT KOCHENDÖRFER [SDK 1953] aufgegriffen. Die Bäcklundtransformationen für weitere Solitonengleichungen wurden erst in jüngerer Zeit erforscht. Z. B. behandelten HUGO WAHLQUIST und FRANK ESTABROOK [Wahl., Esta. 1973] die Bäcklundtransformation der KdV-Gleichung sowie GEORGE LAMB JR. 1974 [Lamb 1974] die Bäcklundtransformation für die mKdV-Gleichung und die Nichtlineare Schrödingergleichung.
Weiter mit Kapitel 4: Solitonen in der Festkörperphysik