[Inhaltsverzeichnis]

Die Solitonentheorie hat im Laufe ihrer etwa 160-jährigen Geschichte mehrfach ihre Gestalt gewechselt. Mehrere verschiedene Wurzeln und Entwicklungslinien konvergierten zu einem Begriff. Nach weit verbreiteter heutiger Auffassung sind zeitkontinuierliche unendlichdimensionale integrable Systeme vom Evolutionstyp Gegenstand der Solitonentheorie. Die daraus abzuleitende naheliegende Vermutung, daß der Ursprung der Solitonentheorie in der Theorie der partiellen Differentialgleichungen liege, ist nur zum Teil richtig. Die Geschichte nahm einen etwas anderen und komplizierteren Weg. Die Solitonentheorie wurde (der Sache nach, zunächst noch nicht dem Wort nach) über das Soliton definiert und nicht über die Solitonengleichung. Ein Soliton wurde ab 1965 eine Lösung oder eine Lösungsschar einer nichtlinearen Evolutionsgleichung genannt, welche anschaulich ein oder mehrere Teilchen beschreibt und die sogenannte Kollisionseigenschaft aufweist [SCM 1973]. Als NORMAN J. ZABUSKY und MARTIN D. KRUSKAL 1965 den Namen Soliton für bestimmte Lösungen der Korteweg-de Vries-Gleichung (KdV-Gleichung) vorschlugen [Zab., Kru. 1965], machten sie damit auf die Teilcheneigenschaften dieser Lösungen aufmerksam. Eigentlich hatten diese Lösungen Solitron heißen sollen, in Anlehnung an Elektron; doch der Name Solitron war bereits rechtlich geschützt und somit ungeeignet. ZABUSKY teilte dazu mit [persönliche Mitteilung]:

"The name "solitron" was the name of an American firm which I believe doesn´t exist today. Although there may be a Japanese company by that name."

In der mehr physikalischen Literatur, insbesondere der Feldtheorie oder Festkörperphysik aber auch der Mathematischen Physik, wurde in den Siebzigern der Begriff Soliton zugunsten physikalischer Modelle "aufgeweicht": Er wurde auf räumlich konzentrierte, nicht-dissipative Lösungen mit endlicher Energie ausgedehnt, auch wenn diese die Kollisionseigenschaft nicht besaßen oder deren Gleichungen nicht integrabel waren [Bishop 1979], [Parsa 1979], [Hasegawa 1990]. Diese Situation der Mehrdeutigkeit wurde schon von KRUSKAL [Kruskal 1978], MIURA [Miura 1978] und anderen [DEGM 1982] kritisiert. Wie auch immer, die Definition einer Solitonengleichung durch die Existenz teilchenartiger Lösungen wird heute mehr und mehr durch das oben genannte Integrabilitätskriterium abgelöst. Die frühe Geschichte der Solitonentheorie, soweit sie sich durch das Soliton - die teilchenartige Lösung - definiert, beginnt bei der Entdeckung solitärer Wellen und der Kollisionseigenschaften. Die eigentliche Etablierung der Solitonentheorie wurde später durch die Erkenntnis bewirkt, daß beide Eigenschaften, Teilcheneigenschaften von Lösungen und Integrabilität der Differentialgleichungen, zusammengehören.

Zur Strukturierung der Geschichte der Solitonentheorie erweist sich ein Modell als besonders geeignet, das in der Wissenschaftstheorie für die Entstehung einer wissenschaftlichen Disziplin vorgeschlagen wurde [Guntau 1982]. Es unterteilt die Geschichte in drei Perioden: eine Vorgeschichte oder frühe Periode, eine klassische und eine moderne Periode. In der Vorgeschichte oder - wie sie hier genannt werden soll - frühen Geschichte existierte die Solitonentheorie noch nicht als einheitliches Gebiet. Wohl wurden einzelne Eigenschaften der Solitonen oder ihrer Gleichungen separat in Einzelarbeiten oder Strängen von aufeinander aufbauenden Arbeiten schon untersucht, doch das vereinheitlichende Konzept blieb verborgen. Das eigentliche Begriffssystem der Solitonentheorie war noch nicht entwickelt. Auf eine Übergangsphase in die hier als klassische Geschichte der Solitonentheorie bezeichnete Periode weist ein Einschnitt in der Entwicklung der Solitonentheorie in den 60er Jahren hin: Es wurden viele physikalische Anwendungen von Solitonengleichungen, hauptsächlich der Sinus-Gordon-Gleichung (SG-Gleichung) und der Korteweg-de Vries-Gleichung (KdV-Gleichung), entdeckt (s. Kapitel 5). In diesen Strom der Entdeckungen wurde die inverse Streumethode (oder auch inverse Streutransformation) - kurz IST - hineingestellt, die 1967 entdeckt wurde und mit der die Integration der KdV-Gleichung und später der SG-Gleichung und weiterer Solitonengleichungen ermöglicht wurde. Diese Synthese von Anwendungen und mathematischer Theorie bewirkte in den 70er Jahren die explizite Herausbildung des neuen Gebietes Solitonentheorie. Eine solche Disziplingenese durch das Zusammenwirken von Experiment und Mathematik ist in der Geschichte der Physik durchaus typisch [Stichweh 1984].

Die in den 70er Jahren beginnende klassische Geschichte der Solitonentheorie brachte die bis dahin noch voneinander unabhängigen Entwicklungslinien der frühen Periode in einen Zusammenhang. Historisch Gewordenes begann man nun zu einer neuen Einheit zu organisieren: Die verschiedenen Eigenschaften der Solitonen oder ihrer Gleichungen, die die Arbeiten aus den verschiedenen Entwicklungslinien der frühen Geschichte der Solitonentheorie z.T. schon beschrieben hatten, wurden nun als Gesamtheit betrachtet. Es entwickelte sich ein übergeordnetes, die Disziplin Solitonentheorie explizit konstituierendes Begriffssystem. Vorher gab es sie als solche nur implizit. Sie konstituierte sich und wurde nun im Detail ausgearbeitet. Im Sinne von THOMAS KUHN kam man in die Periode der normalen Wissenschaft. Nach der anfänglichen Definition des Solitons als solitäre Welle mit Kollisionseigenschaften, die heute noch in der anwendungsorientierten Physik fortlebt, ist in der klassischen Periode eine Solitonengleichung eine nichtlineare Evolutionsgleichung u_t = F(u, u_x, u_xx, ...), die in diesem oder jenem Sinne integrabel ist. Der Vorzugsbegriff der Integrabilität ist die Anwendbarkeit der IST: Eine Evolutionsgleichung ist solitonisch, wenn das Cauchysche Anfangswertproblem auf eine Abfolge gewisser (hochgradig nichttrivialer) linearer Probleme zurückgeführt werden kann. Genauer, es wird die nichtlineare Evolutionsgleichung mit einer linearen Differentialgleichung in Verbindung gebracht und die Zeitentwicklung der abhängigen Variablen u entspricht einer linearen Abbildung von Streudaten der letzteren. Es gibt weitere Ausprägungen von Integrabilität einer Evolutionsgleichung, welche in der Regel untereinander äquivalent sind. (Die genauen Nachweise der Äquivalenz bzw. Nichtäquivalenz sind schwierige und z.T. noch offene Probleme, die hier nicht Gegenstand sein können.)

In der modernen Periode der Solitonentheorie könnte die Eigenschaft der Integrabilität auf eine höhere Abstraktionsstufe - mittels der Theorie unendlichdimensionaler Mannigfaltigkeiten und Liescher Symmetriegruppen - gehoben werden. Nach BENNO FUCHSSTEINER [persönliche Mitteilung] kann eine Evolutionsgleichung Solitonengleichung genannt werden, wenn ihr Vektorfeld Element eines Abelschen Anteils einer Virasoro-Algebra ist. Der Beginn dieser Periode zeichnet sich gerade jetzt ab; die Meinungen gehen auseinander, ob sie schon begonnen hat.

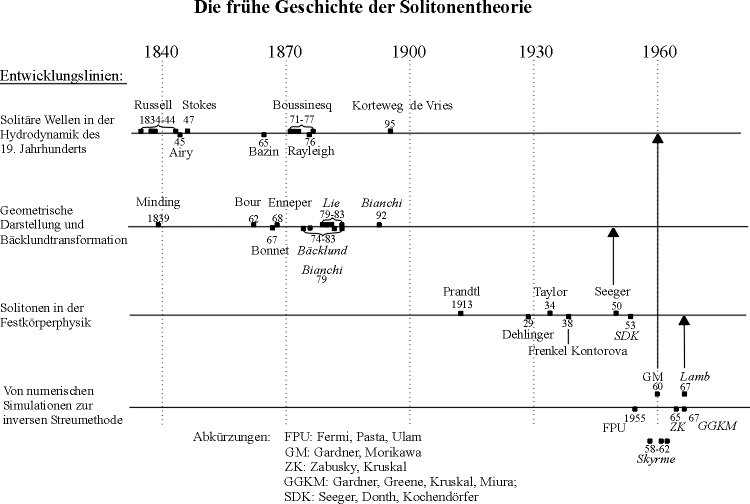
Über diese Gliederung in frühe, klassische und moderne Periode der Solitonentheorie hinaus, denen typische Begriffe zugeordnet werden, wird die Gliederung der ersten oder frühen Periode in vier sogenannte Entwicklungslinien vorgeschlagen. Eine entsprechende Übersicht gibt Abbildung 1.

Übersicht über die frühe Geschichte der Solitonentheorie. Gliederung der wichtigsten Arbeiten in vier zunächst unabhängige Entwicklungslinien, die ab 1950 in Verbindung gebracht werden können und in den siebziger Jahren zur expliziten Entstehung der Solitonentheorie führten. Die vertikalen Pfeile zeigen Querverbindungen zwischen den verschiedenen Entwicklungslinien an. Die kursiven Namen weisen auf Arbeiten hin, in denen nicht nur solitäre Wellen oder eine Solitonengleichung behandelt wurden, sondern für Solitonengleichungen bzw. Solitonen maßgebliche Eigenschaften, also Integrabilität oder Kollisionseigenschaften erkannt worden sind. Neben der Entwicklungslinie "Von numerischen Simulationen zur inversen Streumethode" sind auch von der Linie unabhängige Arbeiten als isolierte Punkte erfasst. Sie sind herausgegriffen aus einer größeren Menge von Arbeiten aus jener Zeit, die zusammen mit der Entwicklungslinie den Übergang zur klassischen Geschichte bilden.

Durch diese Gleiderung wird die einschlägige Literatur mit einer Struktur versehen. In einem kurzen Überblick können die einzelnen Entwicklungslinien wie folgt dargestellt werden:

I. Solitäre Wellen in der Hydrodynamik des 19. Jahrhunderts: Ausgelöst durch die Forschungen JOHN SCOTT RUSSELLs aus den Jahren 1834-44, wurde das Phänomen der solitären Wasserwelle erstmals ausführlich wissenschaftlich erörtert. In der Diskussion über die Natur dieser Welle stritten RUSSELL, GEORGE BIDDELL AIRY, GEORGE GABRIEL STOKES und andere darüber, ob diese Art von Wasserwellen tatsächlich ein unbekanntes Phänomen ist oder nur eine Modifikation der bekannten periodischen Wellen. In Frankreich wurde dieser Streit 1865 durch Experimente EMILE BAZINs und 1872 durch die ausführlichen theoretischen Arbeiten JOSEPH BOUSSINESQs zugunsten RUSSELLs entschieden. In ihnen leitete BOUSSINESQ die Solitonengleichung her, die heute nach ihm Boussinesqgleichung genannt wird. Mangelnde Kommunikation zwischen der französischen und britischen Wissenschaft führte zu weiteren Problemlösungen durch Lord RAYLEIGH und J. McCOWAN und schließlich zu dem vorläufig abschließenden und heute allgemein bekannten Beitrag der Niederländer DIETERIK KORTEWEG und GUSTAV DE VRIES von 1895, in dem sie die später nach ihnen benannte Korteweg-de Vries-Gleichung vorstellten. Beide Gleichungen gerieten danach für etwa 70 Jahre in Vergessenheit!

II. Differentialgeometrische Darstellung und Bäcklundtransformation: Verschiedene Autoren, FERDINAND MINDING und andere, widmeten sich der Erforschung der pseudosphärischen Flächen. (Sie werden in Kapitel 3.1 definiert.) Bei der analytischen Betrachtung pseudosphärischer Flächen gelangten zwei Mathematiker fast gleichzeitig und voneinander unabhängig zur SG-Gleichung. OSSIAN BONNET erwähnte sie 1867 und ALFRED ENNEPER folgte 1868. Die erste Erwähnung fand die SG-Gleichung aber bei EDMOND BOUR, der sie 1862 innerhalb seiner Studien der geodätischen Krümmung einer Fläche herleitete.

In der Abfolge der Arbeiten von LUIGI BIANCHI, SOPHUS LIE und ALBERT VICTOR BÄCKLUND wurde die einparametrige Bäcklundtransformation entwickelt, mit dem Ziel einer Flächentransformation, die die Beschreibung aller pseudosphärischen Flächen erlaubt. Kurz darauf entdeckte BIANCHI ein nichtlineares Superpositionsprinzip, dessen physikalische Bedeutung jedoch vorerst verborgen blieb. In der Differentialgeometrie wurden später weitere Gleichungen entdeckt, die erst in neuerer Zeit als Solitonengleichungen erkannt wurden, sowie Integrationsverfahren, die mit dem Aufkommen der Solitonentheorie zusätzliche Bedeutung erlangten. Diese spielten jedoch historisch, d.h. bei den Entwicklungen, die schließlich zur Solitonentheorie führten, keine Rolle und werden daher im Kapitel zur entsprechenden Entwicklungslinie nur kurz angesprochen.

III. Solitonen als Teilchenmodelle in der Festkörperphysik: Aufbauend auf Modellen von ULRICH DEHLINGER und GEOFFREY INGRAM TAYLOR gelangten JACOV IL'I_ FRENKEL' und TATJANA ABRAMOVNA KONTOROVA bei der Betrachtung von Versetzungen in Kristallen zu dem heute so genannten Frenkel-Kontorova-Modell. Zu dessen Beschreibung diente eine räumlich diskretisierte SG-Gleichung, von der FRENKEL und KONTOROVA zur Ein-Solitonenlösung der SG-Gleichung gelangten. Bei der Weiterentwicklung des Frenkel-Kontorova-Modells stieß ALFRED SEEGER, der die SG-Gleichung zum ersten Mal in einem physikalischen Kontext aufschrieb, auf die Arbeiten der Differentialgeometrie des vorigen Jahrhunderts. Mit dem Werkzeug der Bäcklundtransformation konnte er die SG-Gleichung lösen und erkannte deren große Bedeutung für die Physik.

IV. Von numerischen Simulationen zur IST: Diese Entwicklungslinie schließt die frühe Geschichte der Solitonentheorie ab. Sie ist im wesentlichen bereits historisch erforscht. ENRICO FERMI, JOHN PASTA und STANISLAV ULAM führten 1955 numerische Experimente mit einer Kette von nichtlinear gekoppelten Massepunkten durch. Diese Computerexperimente wurden von NORMAN ZABUSKY und MARTIN KRUSKAL fortgeführt und 1965 in Verbindung mit der KdV-Gleichung gebracht. Im Jahre 1967 wurde die KdV-Gleichung mit Hilfe der neuentwickelten IST gelöst. Schnell wurde entdeckt, daß dieses Verfahren auch auf gewisse andere Gleichungen anwendbar ist, d.h. eine ganze Klasse nichtlinearer partieller Differentialgleichungen vom Evolutionstyp lösen kann. Diese Erkenntnisse führten zusammen mit den zur gleichen Zeit neu entdeckten, vielfältigen Anwendungsmöglichkeiten der Solitonen als Teilchenmodelle in verschiedenen Disziplinen der Physik zu einem "Solitonen-Boom".

Weiter mit Kapitel 2: Solitäre Wellen in der Hydrodynamik des 19. Jahrhunderts

[Inhaltsverzeichnis]