4.1 Der Weg zum Frenkel-Kontorova-Modell
Seit der industriellen Revolution wurde ein immer genaueres Verständnis der inneren Struktur der Metalle benötigt. Besondere Bedeutung kam dabei dem Mechanismus der plastischen Verformung der Metalle zu. Die großen Erfolge der molekularen Theorie der Gase und der Lösungen und die Theorie des thermischen Verhaltens der Festkörper rechtfertigten die Annahme, daß das Verständnis der plastischen Verformung auf der Grundlage des molekularen Modells zu erreichen sei. Nach der Entstehung der Raumgittertheorien, die die Vorstellung des Kristalls schufen, wurde die molekulare Theorie der Elastizität für vollkommen elastische Körper entwickelt. Eine Erklärung der Verformung und Viskosität der Kristalle bereitete jedoch Schwierigkeiten [Kármán 1913]. Gestützt auf Beobachtungen wußte man, daß die meisten Metalle und Gesteine aus kleinen Kristalliten bestehen, und daß diese "kristallinen Haufwerke" im allgemeinen ungemein stärkere Nachwirkungen auf äußere Kräfte zeigten als isomorphe Einzelkristalle. Das legte den Gedanken nahe, daß sich die für die Verformung nötigen Verschiebungen der Atome in festen Körpern hauptsächlich an den Grenzflächen der Kristallite abspielten. Im Jahre 1913 veröffentlichte THÉODOR VON KÁRMÁN (1881 - 1963) [Kármán 1913] ein bis dahin, nach seinen eigenen Worten, unveröffentlichtes Modell von LUDWIG PRANDTL (1875 - 1953), das große Vorzüge aufwies: Das Modell nutzte die Grenzfläche zwischen Kristalliten für einen Erklärungsansatz der plastischen Deformation und konnte auch die Wärmebewegung der einzelnen Atome sowie die Hysterese verständlich machen. PRANDTL legte seinem Modell der Grenzfläche zwischen zwei Kristalliten eine Reihe von Vereinfachungen zu Grunde. Aus der räumlichen Struktur wurden zwei aneinander stoßende Gitterflächen herausgegriffen (s. Abb. 4.1). Als das Wesentliche der so entstandenen eindimensionalen Grenze betrachtete er nur die diese Grenze direkt berührenden Atome.

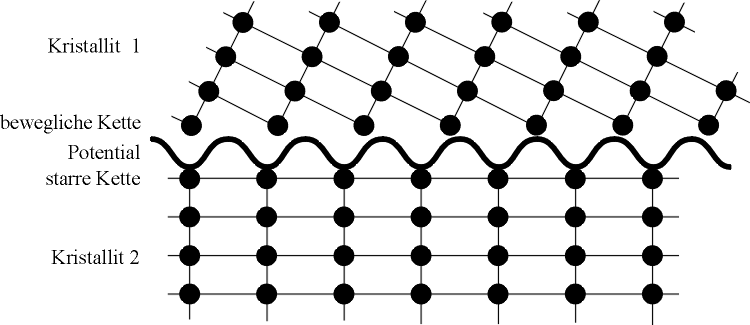
Abbildung 4.1:
Das Prandtlsche Modell der Grenzfläche zwischen zwei Kristalliten 1 und 2. Das Potential der als starr angenommenen unteren Kette übt eine Kraft auf die beweglichen Atome der oberen Kette aus. Sie sind in der Abbildung somit nicht in der Gleichgewichtsposition.
Es entsteht so ein Modell, welches aus zwei Atomketten verschiedener Gitterkonstanten besteht. In diesem Modell wurden die Atome der unteren Kette als starr angenommen. Die untere Atomkette übt somit auf die Atome der oberen Kette eine Kraft aus, die wegen der Starrheit der unteren Kette eine periodische Funktion des Ortes ist. Der Einfachheit halber nahm PRANDTL hierfür eine Sinusfunktion. Die Atome der beweglichen Kette suchen sich nun eine Gleichgewichtslage, die sich aus den Kräften ergibt, die auf sie ausgeübt werden - der der Auslenkung proportionalen Kraft innerhalb der Kette nach dem Hookschen Gesetz und der sinusförmigen Kraft der unteren Kette, wobei nur Auslenkungen in der Richtung der Kette zugelassen wurden. Der Abstand der Atome untereinander in der oberen Kette ist in der Gleichgewichtsposition nun nicht mehr gleich. Eine elastische Deformation des Kristalls bewirkt zuerst, daß die beiden Kristallite, also in der Vereinfachung die beiden Ketten, aneinander entlang durch Einwirken äußerer Kräfte verschoben werden. Die Elastizitätsgrenze des Kristalls wird erreicht, sobald ein Atom der Grenzlinie über einen "Berg" des periodischen Potentials geschoben wird. Es wird ein Stück weit "herunterfallen" und in die gleiche Richtung drücken wie die äußere Kraft. Bei weiterer Deformation werden nun immer gleich viele Atome über ihren nächsten Potentialberg geschoben; d.h. die Deformation geschieht mit konstanter äußerer Kraft, so wie es die Ergebnisse der Experimente verlangten.
PRANDTL lieferte hiermit eine erste Erklärung für den experimentell längst bekannten Befund, daß die mechanische Belastbarkeit von Metallen weit niedriger ist, als es Berechnungen für ideale Kristalle forderten. In diesen Berechnungen wurde angenommen, daß alle Atome gleichzeitig über die "Potentialberge" gedrückt werden müssen. PRANDTLs Modell verband außerdem die Vorstellung, daß Bewegung in Metallen an den Grenzflächen zwischen Kristalliten stattfindet, mit den Gedanken LORD KELVINS. Dieser hatte 1904 [Kelvin 1904] mögliche Gleichgewichtslagen eines eindimensionalen Modells betrachtet, unter der Annahme eines räumlich periodischen Kraftgesetzes. Die Ausführungen, die KÁRMÁN über das Prandtlsche Modell machte, verbleiben ganz in der qualitativen Betrachtung. Auch PRANDTL, der 1928 selbst eine Arbeit zu diesem Thema verfaßte [Prandtl 1928], blieb in diesem Punkt ganz in der Vorstellung und formulierte keine mathematischen Gleichungen.
Das Problem der Kristallplastizität und dessen Lösungsansatz via Grenzflächen zwischen Kristalliten beschäftigte zu dieser Zeit weitere Autoren, u.a. M. POLANYI [Polanyi 1925] und JACOV IL'IC FRENKEL' [Frenkel 1926]. Eine wichtige Vorarbeit in Richtung der SG-Gleichung wurde 1929 von ULRICH DEHLINGER (1901 - 1981) in seiner Habilitationsschrift geleistet [Dehlinger 1929]. DEHLINGER kam unabhängig von PRANDTL, wie er anmerkte, zu einem ganz ähnlichen Modell, lieferte jedoch im Gegensatz zu PRANDTL auch eine mathematische Beschreibung. DEHLINGER betrachtete wie PRANDTL zwei parallele Atomketten an der Grenze zweier sich gegeneinander bewegender Kristallite. Der Gitterabstand sei nun allerdings bei beiden Ketten gleich (s. Abb. 4.2). Auch er meinte, daß ein sinusförmiges Energiepotential der Periodizität des Kristalls am ehesten Rechnung trüge.
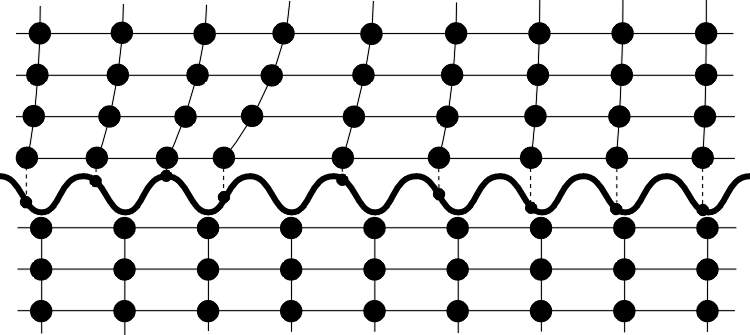
Abbildung 4.2:
Verhakung nach DEHLINGER. Ein Atom der beweglichen Kette ist durch eine temporäre äußere Kraft über einen Potentialberg gedrückt worden und dort verblieben.
Sein Modell (s. Abb. 4.2) erklärt sich wie folgt: Durch eine Bewegung des oberen Kristallits nach rechts um einen oder mehrere Atomabstände hinweg wurden die oberen Atome gemeinsam über die "Potentialberge" gedrückt. Ein Atom sei dabei zurückgeblieben, sei also nicht über den Potentialberg gekommen. Aus dieser Postition drückt es seine Nachbaratome nach links. Die Störung, DEHLINGER nannte es eine Verhakung, wirkt sich um so weniger aus, je weiter die Atome von ihr entfernt sind. Entstehen durch die Verformung des Metalls Verhakungen in großer Zahl, so tragen sie nach DEHLINGER dazu bei, daß die Grenzflächen leichter aneinander entlang gleiten. Für DEHLINGER waren sie eine Erklärung dafür, daß die mechanische Belastbarkeit vieler Metalle weit niedriger ist, als es Berechnungen für ideale Kristalle vermuten lassen.
Um zu quantitativen Ergebnissen zu gelangen, stellte DEHLINGER die Gleichgewichtsbedingung des n-ten Atoms der beweglichen Kette auf. Das periodische Potential setzte er gleich
![]() (4.1)
(4.1)
wobei qn = Auslenkung des n-ten Atoms aus der Position des idealen Gitters, a = Gitterabstand, 2A = Potentialmaximum. Aufgrund des Hookschen Gesetzes ergibt sich die Gleichgewichtsbedingung
![]()
oder
![]() (4.2)
(4.2)
Eine recht ausführliche Behandlung der Arbeiten LUDWIG PRANDTLs und ULRICH DEHLINGERs findet sich bei ALFRED SEEGER [Seeger 1980a, b]. In [Seeger 1983] ist auch eine kurze Beschreibung von Arbeiten anderer Autoren zur Kristallplastizität.
Auf DEHLINGERs Vorstellungen zur Beschreibung von Verhakungen kam wenige Jahre später u.a. GEOFFREY INGRAM TAYLOR (1886 - 1975) zurück [Taylor 1934]. Im Jahre 1934 betrachteten TAYLOR, E. OROWAN und M. POLANYI unabhängig voneinander wandernde Versetzungen [Seeger 1983]. (Versetzung eben deshalb, weil ein ganzer Teil des Kristalls gegenüber einem anderen Teil durch das Wandern der Fehlstelle entlang der Grenze um einen oder mehrere Gitterplätze versetzt wird.) Wie PRANDTL und DEHLINGER griff TAYLOR aus einem zweidimensionalen Kristallgitter zwei benachbarte Atomketten heraus, die sich aneinander entlang bewegen.
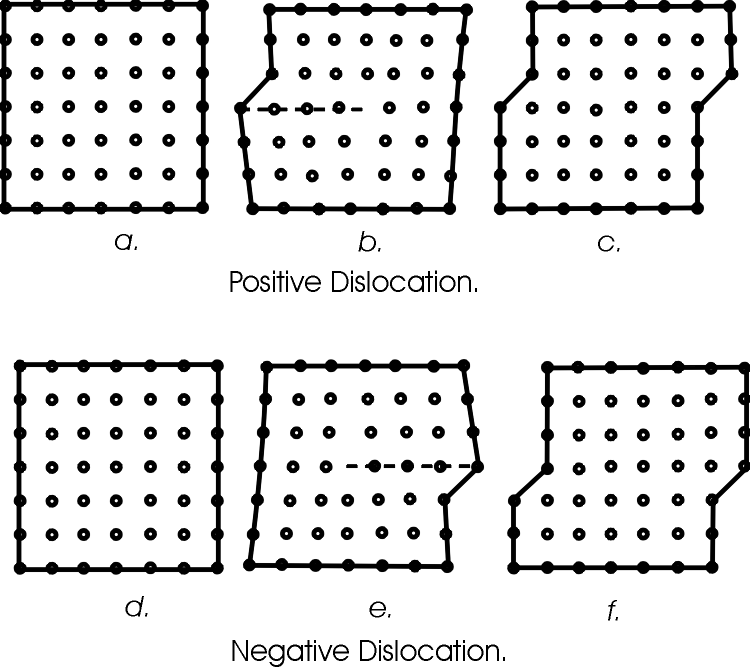
Abbildung 4.3:
Positive und negative Versetzung nach TAYLOR. Aus [Taylor 1934].
Diese Bewegung bewirkt eine einfache Schiebung, wie es zu der Zeit bezeichnet wurde; man kann es als Scherung im Kristallit betrachten. Eine durch Temperaturbewegung oder Spannung im Kristall hervorgerufene Versetzung äußert sich nach TAYLOR darin, daß eine Atomkette auseinandergezogen, und die andere zusammengedrückt wird (s. Abb. 4.3). Die so in der auseinandergezogenen Kette entstandene Lücke kann nun durch den Kristall wandern, bei der positiven Versetzung in Abb. 4.3 von links nach rechts, bei der negativen von rechts nach links.
Der Vorstellung, daß die durch den Kristall laufende Versetzung nur aus einer einzigen Lücke in der auseinandergezogenen Kette bestehen soll, widersprach 1938 der Professor für Theoretische Physik des Leningrader Physikalisch-Technischen Instituts JAKOV IL'IC FRENKEL' in einer zusammen mit seiner Assistentin TATJANA ABRAMOVNA KONTOROVA geschriebenen dreiteiligen Arbeit [Fre., Kon. 1938]. FRENKEL und KONTOROVA (im weiteren: F & K) waren der Meinung, daß die bei TAYLOR beschriebene Versetzung sich nur dann fortbewegt, wenn keine einzelne Lücke in der auseinandergezogenen Kette vorliegt, sondern sich die Kette in einer mehr kontinuierlichen Form auseinanderzieht (s. Abb. 4.4).
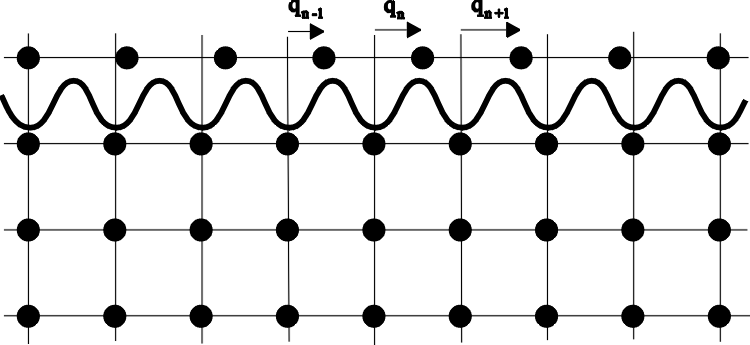
Abbildung 4.4:
Lang auseinandergezogene Versetzung des Frenkel-Kontorova-Modells.
Dieser Vorstellung entspricht eine stärkere Kopplung der Atome innerhalb der Atomketten gegenüber einem schwächeren sinusförmigen Potential zwischen den verschobenen Ketten. F & K zeigten in ausführlichen Rechnungen und Vergleichen, daß diese Vorstellung vorzüglich mit experimentellen Befunden übereinstimmte [Fre., Kon. 1938, Teil II] und somit die Annahme einer langgezogenen Versetzung berechtigt war. Sie griffen auch das von TAYLOR erwähnte Wandern der Versetzung auf und befaßten sich im Wesentlichen im ganzen ersten Teil ihrer Arbeit mit der Dynamik der Versetzungen, d.h. mit der Dynamik der Atome der beweglichen Kette. Sie gingen vom gleichen Ansatz wie DEHLINGER 1929 aus, machten allerdings aus DEHLINGERs statischer Gleichung (Gleichung (4.2)) eine Bewegungsgleichung:
![]() (4.3)
(4.3)
Ob FRENKEL DEHLINGERs Habilitationsarbeit [Dehlinger 1929] bekannt war, ist nicht klar. Dafür spricht, auch wenn er sie nicht direkt zitierte, daß sie von TAYLOR 1934 erwähnt wurde [Taylor 1934], dessen Arbeit F & K ihren Studien gegenüberstellten. FRENKEL legte besonderen Wert auf das genaue Studium der gesamten Fachliteratur, insbesondere der zur Festkörperphysik [Tamm 1962], [Frenkel 1974]. Andererseits ist der einleitende Satz zum ersten Teil der Arbeit nicht ganz richtig, was F & K, hätten sie DEHLINGERS oder PRANDTLs Arbeiten gekannt, gewußt hätten. Der Satz lautet [Fre., Kon. 1938, Teil 1, S. 89, Übersetzung von R. Schimming]:
"Bis zu den Arbeiten von Taylor hat man gewöhnlich angenommen, daß die plastische Verformung von Kristallen mittels einer Verschiebung eines Teils des Kristalls als Ganzem relativ zu einem anderen Teil realisiert wird, wobei man voraussetzte, daß diese Verschiebung nur in einer Ebene stattfindet und gleichzeitig in der Gesamtheit dieser Ebene."
Schon DEHLINGER und PRANDTL hatten mit dieser Ansicht gebrochen (s.o.).
F & K gelang es, Gleichung (4.3) näherungsweise durch geschickte Annahmen zu lösen. Dieser Weg sei hier kurz skizziert. Sie setzten den reibungsfreien Gleitprozess voraus: "Rutscht" ein Atom der beweglichen Kette aus seinem Gitterplatz etwa nach rechts auf den nächsten Gitterplatz (s. Abb. 4.4, erstes Atom von rechts in der beweglichen Kette relativ zum ersten Atom von links), so zieht es durch die Kopplung innerhalb der beweglich Kette die Atome links von sich nach rechts hinter sich her. Als Folge davon wandert die ganze Versetzung nach rechts. Da F & K nur zwei Ketten betrachteten, wovon eine wie bei DEHLINGER fest und unbeweglich sein sollte, kann solch eine Wanderung reibungsfrei verlaufen. Dies setzten F & K voraus und setzten
![]()
(4.4)
Dabei ist τ die Zeit, die die Versetzung benötigt, um einen Gitterplatz weiter zu wandern. Die Wanderungsgeschwindigkeit ist somit v = a/τ (mit a = Gitterkonstante). Damit wird Gleichung (4.3) zu
![]()
F & K entwickelten diese Gleichung in eine Taylorreihe bezüglich τ und brachen nach dem quadratischen Term ab. Als Bedingung für diesen Schritt forderten sie, daß die Funktion q sich während der Zeit τ nur wenig verändern sollte. Diese Forderung beinhaltet, daß sich die Versetzung über viele Gitterplätze erstreckt, wie F & K es in Opposition zu TAYLOR einleitend angenommen und im Experiment bestätigt gefunden hatten. Auf diese Weise erhielten sie eine gewöhnliche Differentialgleichung:
![]() (4.5)
(4.5)
mit einer neuen "formalen" Masse m´ = m - Cτ2. Diese Gleichung hat die Form der Bewegungsgleichung des Fadenpendels, wobei aber m´ beliebiges Vorzeichen haben kann. F & K erhielten sowohl für m´ > 0 als auch für m´ < 0 Lösungen. Für m´ > 0 beschreiben diese Lösungen kleine Oszillationen um die Ruhelage. Als eine Lösung für m´< 0, erhielten F & K
![]() (4.6)
(4.6)
mit einer Integrationskonstante C0, die den zeitlichen Nullpunkt festlegt. Die Voraussetzung der gleichförmigen Bewegung (Gleichung 4.4) genügten F & K, um die statische Lösung (4.6) in eine bewegte übergehen zu lassen:
![]() (4.7)
(4.7)
Diese Lösung ist die Ein-Solitonenlösung der SG-Gleichung! (Wegen Gleichung (4.4), also v = const. = a/τ gilt nτ = n a/v = x/v.) Dies scheint zuerst verwunderlich, da die Differential-Differenzengleichung (4.3), von der F & K ausgingen, sich von der SG-Gleichung durch die Diskretheit der Ortsvariablen unterscheidet. Eine kontinuierliche Ortsvariable (q = q(x,t)) hätte direkt zur SG-Gleichung geführt
![]()
Dieser Schritt der Kontinuisierung ist von F & K implizit durch die Forderung gemacht worden, daß qn sich nur wenig ändern sollte im Laufe der Zeit τ, die Versetzung also langgestreckt, kontinuierlich sein sollte. Die besonderen Eigenschaften dieser Lösung als Soliton blieben F & K allerdings verborgen, bis auf die gleichbleibende Bewegung der Versetzung durch den Kristall. Doch diese konnte sie nicht verwundern, da sie als Forderung in den Lösungsweg mit eingegangen war.
Die Arbeit von F & K ist durchaus kein Zufallsprodukt, sondern in einen langen Kontext in FRENKELs Lebenslauf eingebunden. Das Diskrete in seinen verschiedensten Formen, diskrete Verteilungen, diskrete Massen an Ketten, waren eins seiner "Lieblingsthemen", denen er sich immer wieder widmete [V. Ja. Frenkel (Sohn von Ja. I. Frenkel), persönliche Mitteilungen]. Schon mit 16 Jahren entwickelte er eine Verallgemeinerung der Reihentheorie und zeigte sie dem St.Petersburger Universitätsprofessor Ja. V. USPENSKIJ. Dieser fand darin die Grundzüge der Rechenmethode der finiten Differenzen, die USPENSKIJs Lehrer A. A. MARKOV nicht lange vorher entwickelt hatte [Frenkel 1974]. Die aktuellen Fragen der Kristallphysik in den dreißiger Jahren, speziell die der Härte und Elastizität von Kristallen, wurden intensiv von A. F. JOFFE untersucht. FRENKEL, der auch in dem von JOFFE gegründeten Leningrader Physikalisch-Technischen Institut (LFTI) arbeitete, kam daher mit diesen Problemstellungen intensiv in Verbindung und widmete sich ihnen auch ausführlich. An diesem Institut wurden auch viele Versuche zu Fehlstellen in Kristallen gemacht; u.a. untersuchte JOFFE die Bruchfestigkeit und Elastizität von Kristallen, deren Oberfläche er an einer Stelle mit Säure behandelte. Wie er feststellte, waren die so behandelten Stellen wesentlich zäher und stabiler gegenüber Deformation und Bruch als die unbehandelten Stellen [V. Ja. Frenkel, pers. Mitt.]. Die Theorie zu diesen Versuchen überließ FRENKEL seiner Assistentin KONTOROVA als Doktorarbeit mit dem Thema "Statistische Theorie der Festigkeit von Kristallen" [Kontorova 1938]. Aus dieser Arbeit ging der Artikel [Fre., Kon. 1938] hervor. FRENKEL hatte daher sehr detaillierte Kenntnisse speziell zur Theorie der Elastizität und Deformierbarkeit von Kristallen und den damit in Verbindung gebrachten Versetzungen. Trotz dieser Kenntnisse waren sich F & K der großen Bedeutung der Versetzungen für die Plastizität der Metalle wohl nicht bewußt [Fre., Kon. 1938, Teil 2, aus Frenkel, ges. Werke, S. 372]. Das ist nicht verwunderlich, denn abgesehen von wenigen Autoren, die darauf hinwiesen, daß die Versetzungen die maßgebliche Rolle bei der plastischen Deformation von Metallen spielen [Bur., Bur. 1935], [Kochendörfer 1937], war diese Tatsache in den 30er Jahren noch nicht bekannt [Seeger, pers. Mitt.]. Die Theorie der Versetzungen befand sich noch in den Anfängen. Auf die Bedeutung der Versetzungen und insbesondere ihrer Dynamik wiesen 1940 DEHLINGER und ALBERT KOCHENDÖRFER (1908 - 1995) hin [Dehl., Koch. 1940]. Im Titel ihrer Arbeit [Dehl., Koch. 1940] nannten sie die bewegten Versetzungen Eigenbewegungen und wiesen damit auf die Verwandschaft der Versetzungsbewegungen mit den gewöhnlichen Eigenschwingungen eines Kristallgitters hin. Während die Eigenschwingungen aus dem quadratischen Ansatz des Kristallpotentials resultieren, entstehen die sogenannten Eigenbewegungen durch die Periodizität des Kristallpotentials.
Daß FRENKEL die bedeutungsvolle Arbeit an wandernden Versetzungen zu keinem späteren Zeitpunkt wieder aufnahm, kann mehrere Gründe haben. Zum einen schien er die Bedeutung der Versetzungen nicht erkannt zu haben. Zum anderen kann es daran liegen, daß er, mag man die Klassifizierung W. OSTWALDs in seinem Buch "Große Männer" nehmen, ein "romantischer" Wissenschaftler war [Tamm 1962], [Frenkel 1974]. Es lag zum einen nicht in seiner Linie, sich ausführlich mit Details eines Problems auseinanderzusetzen. Und zum anderen beschäftigte er sich in seinen produktivsten Jahren 1938-39 - an der Zahl seiner Veröffentlichung gemessen - mit einer außerordentlichen Zahl und Weite von Themen, die ein In-die-Tiefe-Gehen kaum zuließ. Keinesfalls liegt es daran, daß die Theorie der Versetzungen während der Zeiten des Stalinismus aus ideologischen Gründen in Verruf geraten war. Daß sie in Verruf geraten war, belegen zwei Hinweise. SEEGER [pers. Mitt.] bemerkte, daß 1955, zu Beginn der "Tauwetterperiode", der sowjetische Wissenschaftler ODING nach Stuttgart kam und um "Starthilfe" in der Theorie der Versetzungen bat. Die Versetzungen, teilte er mit, hatten bis dato nicht in die Ideologie gepaßt, weshalb die Sowjetunion nun in dieser Beziehung ins Hintertreffen gelangt sei. Die technische Relevanz und wohl nicht zuletzt der spätere Einsatz des in der Sowjetunion sehr bekannten Mathematikers SEDOV für die Versetzungen verhalfen der Theorie der Versetzungen zur Rehabilitation. Der zweite Hinweis kommt von V. Ja. FRENKEL [Frenkel, pers. Mitt.]. Angeregt wohl durch KONTOROVA selber, die im Gegensatz zu FRENKEL Parteimitglied war, geriet die Theorie der Versetzungen etwa 1945 in ideologische Diskussionen. KONTOROVA hatte sich in dieser Zeit sehr mit dem Dialektischen Materialismus und dessen Rolle in der Physik beschäftigt. In ihrem Nachlaß fanden sich allein zehn Notizbücher zu diesem Themengebiet und anderen philosophischen Fragen. Nicht nur wegen des späten Zeitpunktes der "Verurteilung" der Versetzungen wird sie keine Rolle bei FRENKELs Themenwahl zu seinen Forschungen gespielt haben. Auch stand dieses kleine Detail in keinem Verhältnis zu FRENKELs Arbeiten zur Relativitäts- und Quantentheorie, die schon viel früher als "bourgeoise Wissenschaft" galten.
Das Frenkel-Kontorova-Modell fand in den folgenden Jahrzehnten in der Festkörperphysik mehrfach Anwendung [Nabarro 1967] und ist bis heute Objekt mancher Forschungen [Aub., Dae. 1983], [Strunz 1995]. Wie sehr das Modell fesseln kann zeigt eine Äußerung des amerikanischen Feldtheoretikers ROBERT HOBART, der in den fünfziger und sechziger Jahren mit beteiligt an der Suche nichtlinearer Feldgleichungen war (s. Kapitel 5.1), eine Suche, die schließlich auch zur SG-Gleichung führte. HOBART schrieb in einem Brief an den Autor dieser Dissertation:
"I've been retired now for three years. My current research is again my thesis problem: Develop analytical tools tailored to calculating the energy barrier to mobility of a discrete Frenkel-Kontorova dislocation. The barrier is essentially singular in the lattice spacing parameter, so the problem can't be solved by perturbation methods."
Weiter zu Kapitel 4.2: Die Sinus-Gordon-Gleichung als Gleichung für wandernde Versetzungen