4.2 Die Sinus-Gordon-Gleichung als Gleichung für
wandernde Versetzungen
Nachdem das Modell der Versetzungen durch die Physiker F & K in Leningrad, DEHLINGER und KOCHENDÖRFER in Stuttgart und TAYLOR und POLANYI in England bis zur Dynamik der Versetzungen vorangetrieben war und durch Experimente [Dehl., Koch. 1940] weitgehend bestätigt worden war, unterbrach der 2. Weltkrieg die fruchtbaren internationalen Verbindungen der Forscher. Der deutsche Einmarsch in Rußland 1941 bewirkte eine Isolation der Sowjetwissenschaft, die Reduzierung und Verlegung der Forschung, deren Umstellung auf kriegsrelevante Themen. In Stuttgart wurde von DEHLINGER und KOCHENDÖRFER während des Krieges, soweit dieser es zuließ, weiter an Versetzungen geforscht. Für DEHLINGER stellte die Diskretheit der Atome im Kristall eine wichtige Eigenschaft dar, die beim Studium der Versetzungen (für DEHLINGER waren es ja Verhakungen) nicht außer Acht gelassen werden sollte [Seeger, pers. Mitt.]. Deshalb verfolgte er die Kontinuisierung, die F & K begonnen hatten, nicht weiter.
Im Sommer 1948 regten DEHLINGER und KOCHENDÖRFER den jungen Studenten der TH Stuttgart ALFRED SEEGER an, im Rahmen seiner Diplomarbeit das dynamische Modell der Versetzungen weiter zu untersuchen. Das Modell von F & K sollte verallgemeinert werden für den Fall, daß die obere bewegliche und die untere feste Atomkette verschiedene Gitterkonstanten hatten, und es sollte genauer ausgearbeitet werden [Seeger, pers. Mitt.]. Da bei zwei verschiedenen Gitterkonstanten die beweglichen Atome auch ohne Versetzung nicht äquidistant sind (wie schon PRANDTL gezeigt hatte), ließ SEEGER neben der Verschiebungskoordinate qn(t) noch die Anfangslage zn0 zu, die die Abweichung der Ruhelage des n-ten Atoms von der Äquidistanz beschreibt. So kam er zu der gegenüber Gleichung (4.3) leicht modifizierten Gleichung
![]()
(4.8)
SEEGERs Absicht war es, den Ansatz von F & K nicht nur zu generalisieren, indem er verschiedene Gitterkonstanten zuließ, sondern die F & K-Gleichung auch allgemein zu lösen, ohne viele Annahmen machen zu müssen. Es hatte sich schnell gezeigt, daß die Annahmen, die FRENKEL in das System hineinstecken mußte, um zur lösbaren Bewegungsgleichung (4.5) zu kommen, sehr speziell waren und eine Verallgemeinerung nicht zuließen [See., Koch. 1950]. Zu diesem Zweck trennte er die beiden Haupteigenschaften eines Kristallgitters, die Periodizität und die Diskretheit der einzelnen Atome. Für SEEGER war - im Gegensatz zu DEHLINGER - die Periodizität des Kristalls die wichtigere Eigenschaft, wohingegen die Diskretheit aufgegeben werden konnte, da auch das periodische Potential nicht diskret ist [Seeger, pers. Mitt.]. SEEGER baute auf FRENKELs Vorstellung auf, daß sich die Versetzung über mehrere Gitterabstände erstreckt. Das erlaubte es ihm, auf die für die Dehlingerschen Verhakungen noch wichtige Diskretheit der Atome zu verzichten und eine Kontinuisierung der Ortskoordinate durchzuführen (s. Abb. 4.5). Die diskrete Variable qn(t) ersetzte er durch die kontinuierliche Variable q(n,t) gemäß der Approximation
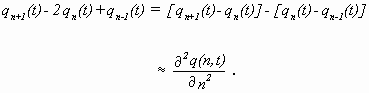
Diese Näherung hätte es direkt erlaubt, Gleichung (4.8) in eine Differentialgleichung überzuführen. SEEGER beschritt jedoch den Weg über das Hamiltonsche Variationsprinzip und gab die potentielle und kinetische Energie des Systems vor. Als Euler-Lagrange-Gleichungen erhielt er
![]() (4.9)
(4.9)
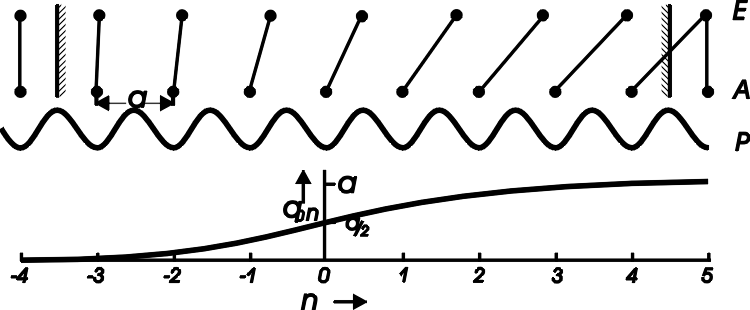
Abbildung 4.5:
Abbildung aus der auch aus A. SEEGERs Diplomarbeit hervorgegangenen Veröffentlichung [See., Koch 1950]. Unten: Verlauf der Atomverschiebung q0n einer ruhenden Versetzung (der Index 0 steht für v = 0) in Abhängigkeit von der Atomnummer n für eine Versetzung im Falle gleicher Gitterkonstanten, also a = α, berechnet nach (4.6). Oben: Potentialverlauf P; Anfangslagen A der Atome in den Potentialmulden; Endlagen E der Atome. Die senkrechten schraffierten Linien geben die Länge der Versetzung an.
Die Gitterkonstante α anstatt a aus Gleichung (4.8) trägt der Tatsache Rechnung, daß die maximale Verschiebung der Atome durch die Versetzung eine Periode α des Potentials beträgt. Mit der Variablentransformation
![]()
nimmt Gleichung (4.9) die Form an
![]() (4.10)
(4.10)
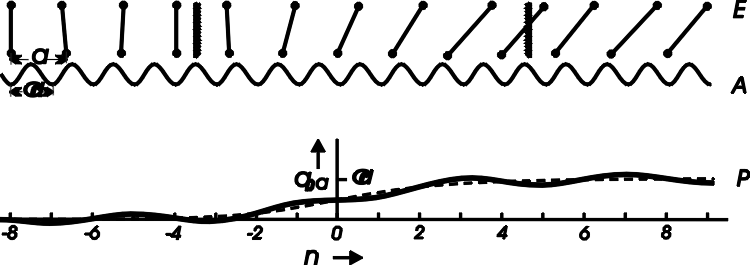
Abbildung 4.6:
Wie Abb. 4.5, nur für den Fall a ¹ α. Die gestrichelte Linie gibt den mittleren Verlauf an, der einer Versetzung nach Abb. 4.5 entspricht.
Die nicht äquidistanten Ruhelagen der Atome bei verschiedenen Gitterkonstanten, die in Z0(x) der Gleichung (4.10) sichtbar wird, bereiteten arge Probleme beim Lösen dieser Gleichung, so daß sich SEEGER in seiner Diplomarbeit nur um Lösungen für Z0 = 0 bemühte. Für Z0 = 0 geht Gleichung (4.10) in die SG-Gleichung über, die auf diese Weise zum ersten Mal in einem physikalischen Kontext aufgeschrieben wurde:
![]() (4.11)
(4.11)
Zur Lösung dieser Gleichung wandte SEEGER die Lie- bzw. Lorentztransformation an. Ihm war bekannt, daß alle Gleichungen der Form uxx - uyy = f(u) lorentzinvariant sind. Also löste er die zeitfreie Gleichung
![]() (4.12)
(4.12)
die Gleichung für ruhende Versetzungen, um sie dann mittels Lorentztransformation wieder zeitabhängig zu machen. u0(ω) wird so zu u(x,y) falls gilt ω = c1x + c2y mit c12 - c22 = 1 und c2 / c1 = v. Damit folgt für die bewegte Versetzung
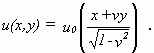 (4.13)
(4.13)
Dabei ist, wie im Folgenden, v in Einheiten der Schallgeschwindigkeit vs angegeben. Zweimalige Integration der Gleichung (4.12) führten SEEGER et al. zu den elliptischen Funktionen [See., Koch. 1950]
![]()
(4.14)
mit: am
= Amplitudenfunktion mit Modul k. Die Integrationskonstante C2 legt den Koordinatenursprung fest. Diese allgemeine statische Lösung ließ für verschiedene Werte des Moduls k (als zweite Integrationskonstante) verschiedene Interpretationen zu. Für den speziellen Fall k = 1 geht sie über in
![]() (4.15)
(4.15)
Diese statische Lösung entspricht für den Fall gleicher Gitterkonstante, also mit α = a, der Frenkelschen Lösung (4.6).
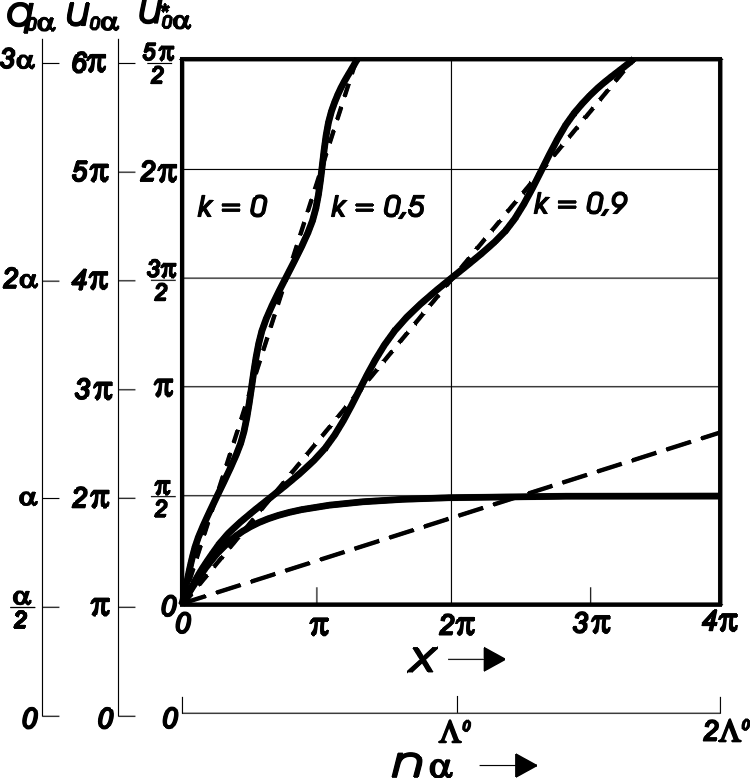
Abbildung 4.7:
Abbildung aus der aus SEEGERs Diplomarbeit [Seeger 1949] hervorgegangenen Veröffentlichung [See., Koch. 1950]. Verlauf der Atomverschiebung u0 bzw. q0 in Abhängigkeit von der Ortskoordinate x bzw. nα nach (4.14). Die Kurven mit k < 1 stellen periodisch angeordnete Versetzungen (in unendlichen Atomreihen) dar. Die gestrichelte Gerade bezeichnet die mittlere Neigungsgerade, bis zu welcher im Falle α = a Versetzungen in endlichen Atomreihen stabil sind. Die Kurve eine einzelnen Versetzung, also mit k = 1, entspricht dem rechten Teil der Kurve aus Abbildung 4.5 bei um α/2 verschobenem Koordinatenursprung.
Somit hatten SEEGERs Bemühungen, den Ansatz so allgemein wie möglich zu halten, den Erfolg allgemeinerer Lösungen als bei F & K. Die allgemeine statische Lösung (4.14) konnten SEEGER et al. mittels der Lorentztransformation in Bewegung versetzen, so daß sie folgende Lösungen erhielten [Seeger 1953]:
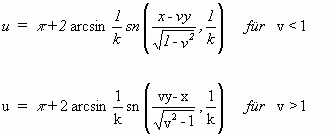
(4.16a)
(4.18a)
Die Konstante k liefert für k ³ 0 reelle Lösungen in beiden Fällen (4.16a, b). Für v < 1 und k < 1 ergeben sich unendliche Reihen gleicher bewegter Versetzungen, die SEEGER et al. schon aus energetischen Gründen nicht für physikalisch hielten. Daher sahen sie nur die bewegte Lösung der Einzelversetzung als physikalisch an, die aus der Schar (4.16a) für k = 1 hervorging:
![]() (4.17)
(4.17)
Aus der Lösungsschar (4.16b) interessierten SEEGER et alias, ebenfalls aus energetischen Gründen, nur die Lösungen mit k > 1. Sie stellten Schwingungen der Atome mit Überschallgeschwindigkeit um ihre Ruhelage dar und glichen den Frenkelschen Lösungen mit m´ > 0. Für k >> 1 wird (4.16b) zu
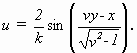 (4.18)
(4.18)
Diese Zustände, die SEEGER gründlich untersuchte [SDK 1953], [Seeger 1953], stellten Schwingungen dar, die abweichendes Verhalten von der linearen Bornschen Gittertheorie zeigten.
SEEGER war kurz nach dem Krieg nicht der Einzige, der - aufbauend auf dem Frenkel-Kontorova-Modell - zur SG-Gleichung vorstieß. Etwa zeitgleich - und auf dem gleichen Wege wie SEEGER über die Taylorschen Versetzungen und das Frenkel-Kontorova-Modell - gelangten in Bristol der Engländer F. C. FRANK und der Südafrikaner J. H. VAN DER MERVE zur SG-Gleichung. In einer vierteiligen Arbeit behandelten sie die SG-Gleichung als Modell für Versetzungen ausführlich [Fra., Mer. 1949a-c, 1950], legten allerdings ihren Schwerpunkt mehr auf die physikalischen Interpretationsmöglichkeiten dieses Modells als auf eine Lösung der SG-Gleichung. Ebenso wie SEEGER behandelten FRANK und VAN DER MERVE zuerst das statische Problem und lösten die Gleichung der Form (4.12) und gelangten zu den Lösungen der Form (4.14) bzw. (4.15). Die Lösung (4.14) für k < 1 interpretierten FRANK und VAN DER MERVE auch als Kette von Versetzungen und zeigten in ihrer ersten Arbeit der vierteiligen Reihe verschiedene der Abb. 4.7 entsprechende Zeichnungen. Ferner lieferten sie viele physikalische Interpretationsmöglichkeiten für die Lösungen (4.14) bzw. (4.15). So sahen sie die Möglichkeit, mit ihnen Versetzungen auf Kristalloberflächen zu beschreiben. Hierbei weist eine Atomkette innerhalb der obersten Atomlage des Kristalls eine Versetzung auf; diese kann innerhalb einer geschlossenen Fläche liegen, oder aber auch die äußerste Kante einer Terrasse bilden. Das Zulassen verschiedener Gitterkonstanten zwischen unbeweglicher und beweglicher Kette erlaubte auch die Interpretation einer Versetzung in einer adsorbierten Monolage aus einer von dem Substrat verschiedenen Substanz. Auch das Modell einer Versetzung innerhalb einer Burgerschen Schraubenversetzung konnten FRANK und VAN DER MERVE in ihre Interpretationen miteinbeziehen. In ihrer zweiten Arbeit der Reihe zu eindimensionalen Versetzungen arbeiteten FRANK und VAN DER MERVE das Modell der Versetzungen in adsorbierten Monolagen aus und erweiterten die statische Gleichung in ihrer dritten Arbeit um einen zweiten harmonischen Term im Potential. Erst in der vierten und letzten Arbeit behandelten sie - ausgehend von der SG-Gleichung - die Dynamik der Versetzungen. Bei der Lösung der SG-Gleichung gingen sie ebenfalls genau so vor, wie es zur gleichen Zeit, jedoch unabhängig, SEEGER tat. Sie stellten (indirekt) die Lorentzinvarianz fest und verfolgten Lösungen der Form (4.14), d.h. sie mußten nur die zeitunabhängige "SG-Gleichung" lösen und die erhaltenen Lösungen mit Hilfe der Gleichung (4.13) zur Bewegung verhelfen.
Der Inhalt der vierten Arbeit von FRANK und VAN DER MERVE ist - wenn man nur die Ergebnisse betrachtet, die die SG-Gleichung und ihre Integration betreffen - mit den Ergebnissen von SEEGERs Diplomarbeit bzw. denen der Arbeit [See., Koc. 1950] vergleichbar. Leider unternahmen sie keine weiteren Integrationsversuche, wie es SEEGER tat. In diesem Zusammenhang ist eine Bemerkung FRANKs und VAN DER MERVEs interessant: In ihrer vierten Arbeit erwähnten sie, daß sie die Arbeit von FRENKEL und KONTOROVA [Fre., Kon., 1938], die ja ähnliche Ergebnisse zur Dynamik aufweist, nicht gekannt hätten, ehe ihre eigenen Untersuchungen abgeschlossen waren. Die Arbeit [Fre., Kon. 1938] hatten sie allerdings schon in ihrer ersten Arbeit zitiert, die im Dezember 1948 eingereicht worden war. Nach dieser Bemerkung haben sie die SG-Gleichung als Modell für die Dynamik von Versetzungen schon 1948 verwendet, zumindest im Kopf. Sie haben damit also zeitgleich mit SEEGER, der seine Diplomarbeit im Sommer 1948 begonnen hatte, die SG-Gleichung in einem physikalischen Kontext gesehen.
Weiter zu Kapitel 4.3: Die Lösung der Sinus-Gordon-Gleichung